Démonstration de la continuité et de la dérivabilité d'une fonction
-
Bbrom2 dernière édition par Hind
Bonjour, j'aimerais avoir de l'aide et une correction pour cet exercice :
Continuité et dérivabilité sur R de f définie par : pour tout x<0, f(x)=cos(pix), pour tout x de [0,2], f(x)=x²+1 et pour tout x>2, f(x)= (2x+1)/(x-1).
J'ai fait :
lim en 0 de f(x)=cos(pix)=1 et lim en 0 de f(x)=x²+1 vaut 1. De plus, f(0)=1 dans les deux expressions donc f(x) est continue (mais pour f(x)=(2x+1/x-1) comment dois je le montrer ? )
Dérivabilité :
f'(x)=-pisin(pix) pour tout x<0 , f'(x)=2x pour x [0,2] et f'(x)=2(x-1)-(2x+1)/(x-1)² pour x>2
ma rédaction n'est pas rigoureuse j'aimerais avoir une rédac type pour ce genre d'exercice...Merci
-
mtschoon dernière édition par

Bonjour,
Rédaction type ? Non , car je ne suis pas prof de fac, mais je peux te proposer une rédaction assez rigoureuse.
Si tu dois fairel'étude sur R, tu pourrais préciser d'abord les cas où il n'y a pas de problème
Sur ]-∞,0[, ]0,2[ et ]2,+∞[ f est définie, continue, dérivable (grâce aux propriétés des fonctions usuelles)
Remarque: la seule condition est x≠1 pour la 3eme expression; cette condition est réalisée, sur l'intervalle considéré.
OK pour la continuité pour x=0
Je regardela continuité pour x=2.
f(2)=22+1=5f(2)=2^2+1=5f(2)=22+1=5
$\lim_{x\to 2\x \lt 2}f(x)=\lim_{x\to 2\x \lt 2}(x^2+1)=2^2+1=5$
$\lim_{x\to 2\x \gt 2}f(x)=\lim_{x\to 2\x \gt 2}\frac{2x+1}{x-1}=\frac{4+1}{2-1}=\frac{5}{1}=5$
Donc :
$\lim_{x\to 2\x \lt 2}f(x)=\lim_{x\to 2\x \gt 2}f(x)=f(2)$
D'où continuité pour x=2
Pour la dérivabilité en 0 et en 2, j'utiliserai la définition de dérivabilité à gauche et à droite en passant par le taux.
-
Bbrom2 dernière édition par
merci
le taux ? je ne vois pas du tout ce que c'est dans ce genre d'exercice.
Donc pour la dérivabilité à gauche et à droite en 0 ou en 2 par contre ?
-
mtschoon dernière édition par

Je te fais l'étude de ladérivabilité en 0, à gauche
Tu sais que f(0)=0²+1=1
$\lim_{h\to 0\h\lt 0}\frac{f(0+h)-f(0)}{h}=\lim_{h\to 0\h\lt 0}\frac{\cos(\pi(0+h))-1}{h}=\lim_{h\to 0\h\lt 0}\frac{\cos(\pi h)-1}{h}$
Pour h voisin de 0, ∏h est voisin de 0 donc
cos(πh)∼1−π2h22\cos(\pi h)\sim 1-\frac{\pi^2h^2}{2}cos(πh)∼1−2π2h2
cos(πh)−1∼−π2h22\cos(\pi h)-1\sim -\frac{\pi^2h^2}{2}cos(πh)−1∼−2π2h2
donc :
$\lim_{h\to 0\h\lt 0}\frac{f(0+h)-f(0)}{h}=\lim_{h\to 0\h\lt 0}\frac{-\frac{\pi^2h^2}{2}}{h}=\lim_{h\to 0\h\lt 0}\frac{-\pi^2h}{2}=0$
Donc :f dérivable à gauche en 0 ; le nombre dérivé à gauche vaut 0
Continue avec l'étude de la dérivée à droite en 0.
Remarque : je pense que tu comprends pourquoi ta méthode proposée n'est pas rigoureuse.
Lorsque tu utilises les fonctions dérivées (valables sur les intervalles) , tu est obligé(e) de chercher la limite des fonctions dérivées lorsque x tend vers 0 et lorsque x tend vers 2( pour trouver f'(0) et f'(2) ).
Cela sous-entend que ces fonctions dérivées sont continues en x=0 et x=2, ce qui n'a pas été prouvé.
-
Bbrom2 dernière édition par
ok à droite : f(x)=x²+1 dois je utiliser cette fonction ou toujours la même que précédemment ?
lim (f(0+h)-f(0))/h = cos(π(0+h))-1/h = cos(πh)-1 / h
on arrive à -π²h²/2 qui tend aussi vers 0.
-
mtschoon dernière édition par

Regarde bien l'énoncé.
Pour la dérivabilité à droite en 0, tu dois utiliser f(x)=x²+1
-
Bbrom2 dernière édition par
d'accord.
Du coup en 0 à droite, la limite vaut 1
On passe d'un limite à gauche qui vaut 0 à une limite à droite qui vaut 1 donc la fonction ne semble pas continue...?
-
mtschoon dernière édition par

Tu écris :"la fonction ne semble pas continue...?"
C'est un mystère pour moi..Que vient faire la continuité la dedans ?
Avec ce qui a été fait précédemment, la fonction est continue sur R.
Tu as écris :Du coup en 0 à droite, la limite vaut 1 : si tu parles du nombre dérivé à droite en 0, c'est faux.
Revois ton calcul (il n'est pas très compliqué)
-
Bbrom2 dernière édition par
Pour la dérivabilité à droite en 0, on utilise f(x)=x²+1
lim (f(0+h)-f(0)/h)=((h²+1)-1)/h)=h²/h=h donc la limite vaut 0 à droite plutôt
-
mtschoon dernière édition par

Oui, cette fois c'est bon.
Je me demande si tu ne confondais pas continuité en 0 avec dérivabilité en 0
Conclusion relative à la dérivabilité pour x=0
f dérivable à gauche en 0 et nombre dérivé à gauche A = 0
f dérivable à droite en 0 et nombre dérivé à droite B = 0Vu queA=B, f est dérivable en 0 et le nombre dérivé vaut : f'(0)=A=B=0
f'(0) (c'est à dire 0) est le coefficient directeur de la tangente (T) à la courbe au point de coordonnées (0,1) . (T) est donc une tangente "horizontale".
Si tu as compris, tu traites maintenant le cas x=2
-
Bbrom2 dernière édition par
ok pour x=2 je dois calculer la limite à droite et à gauche puisqu'on a dit précédemment que f était continue donc :
pour tout x de [0,2], f(x)=x²+1
à gauche :
lim f(2+h)-f(2) / h = ((2+h)²+1 - 5) / h = 4+4h+h²-4 / h = h(h+4)/h= h+4 donc f tend vers 6 quand h tend vers 2 à gauche
à droite :
et pour tout x>2, f(x)= (2x+1)/(x-1) donc :
f(2+h)-f(2) / h = (2(2+h)+1)/(1+h) - 5 / h = (5+2h)/(1+h)-5 / h = (9/3 -5) / 2 =-1à mon avis j'ai du faire une erreur quelque part
-
mtschoon dernière édition par

Ta première phrase est confuse...Tu veux peut-être dire que f(2)=5
Revois tout cela tranquillement.
Pour le nombre dérivé à gauche en 2, tu dois trouver 4
Pour le nombre dérivé à droite en 2, tu dois trouver -3
-
Bbrom2 dernière édition par
je me ramène au calcul de la limite en 0 donc :
f(2+h) - f(2) / h = (2+h)²+1 - 5 / h = 4+4h+h²+1-5 / h = h(4+h) / h = 4+h donc quand h tend vers 0, f tend vers 4à droite :
f(2+h)-f(2) / h = [(2(2+h)+1)/(2+h-1)] - 5 / h = (4+2h+1)/(1+h)-5 / h = (5+2h)/(1+h) -5 /h =0
je ne trouve pas -3 je me suis pourtant relue ...
-
mtschoon dernière édition par

C'est bon pour la dérivabilité à gauche.
A droite, recompte.
Il faut réduire (4+2h+1)/(1+h) et 5 au même dénominateur, et diviser le tout par h
Après simplification, tu dois trouver
f(2+h)−f(2)h=−31+h\frac{f(2+h)-f(2)}{h}=\frac{-3}{1+h}hf(2+h)−f(2)=1+h−3
-
Bbrom2 dernière édition par
ok je vais refaire le calcul.
Une fois que j'en ai déduit toutes ces limites, que dois je dire d'autres ? je ne vois pas le lien entre le 4 et le -3 trouvés en fait...
-
mtschoon dernière édition par

f dérivable à gauche en 2 et nombre dérivé à gauche A = 4
f dérivable à droite en 2 et nombre dérivé à droite B = -34 est le coefficient directeur de la "demi-tangente" à gauche au point de la courbe de coordonnées (2,5)
-3 est le coefficient directeur de la "demi-tangente" à droite au point de la courbe de coordonnées (2,5)4≠-3 donc f n'est pas dérivable pour x=2
Les deux "demis-tangentes"au point de la courbe de coordonnées (2,5) ne constituent pas une droite.
Si tu fais la synthèse de l'étude globale de la dérivabilité de f :
f est dérivable sur R/{2}
**Bilan global de toute cette étude:
f est continue sur R mais dérivable seulement sur R/{2}**
Bonne réflexion !
-
Bbrom2 dernière édition par
ok je vais réfléchir à tout ça...je reviendrai si j'ai des questions
-
mtschoon dernière édition par

D'accord.
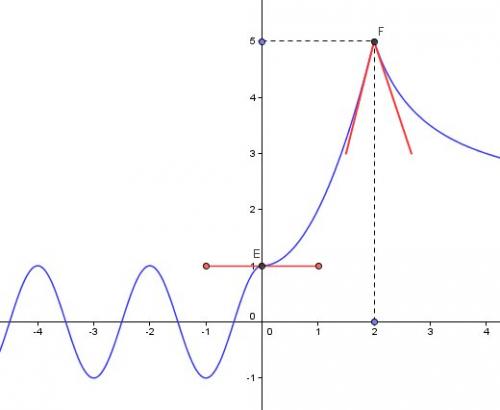
Pour clarifier ta réflexion, je te joins un schéma.
La courbe est en bleu.
L'ébauche de la tangente au point E(0.1) est en rouge
Les ébauches des demis-tangentes au point F(2.5) sont en rougeRemarque ; F s'appelle un point "anguleux" (car nombres dérivés distincts et finis)
-
Bbrom2 dernière édition par
merci beaucoup
-
mtschoon dernière édition par

De rien !
Bon travail.