Système - lecture graphique

[pimousse190408]

Bonjour

Un Producteur de café veut éxpedier par petits containers une partie de sa récolte. On distingue deux variétés de graines différentes :

• L'albina conditionné en sacs de 40 kg, chaque sac ayant un volume de 100 dm 3;
• La kamaro, plus dense, conditionée en sac de 50kg, chaque sacs ayant un volume de 100dm3.

On designe x le nombre de sacs d4albina et par y celui du Kamaro qui son chargés dans le container.

Partie A - Contraintes de volume
Chaque container a un volume de 1 metre cube 1) combien peut on charger dans un container a) de sacs d'Albine b) de sacs de kamaro Justifier chaque reponse. 2) ecrire une énigalité vérifié par les nombres x et y 3) Determiner le nombre de sacs de kamaro que l'on peut charger dans un container qui contient déjà 2 sacs d'Albina.
Partie B - Contraintes de masse
Chaque container ne peut pas supporter une charge plus de 400 kg.

1. Combien de sacs peut on charger dans ce conteiner
   a) De sacs D'Albina
   b)de sacs de kamaro justifier chaque reponse.

2)Ecrire une inégalité vérifié par les nombres x et y.

3. Determiner le nombre de sacs de Kamaro que l'ont peut charger dans un conteiner qui contient déjà 2 sacs d'Albina.

Partie C. Contraintes de volume et de masse
On suppose qu'il existe un changement "idéal"

1. justifier que le couple (x;y) est alors solution du système (S) : {2x+y=10 et 4x+5y=40

2. résoudre ce système

3. commenter cette solution

Partie D Prix de vente

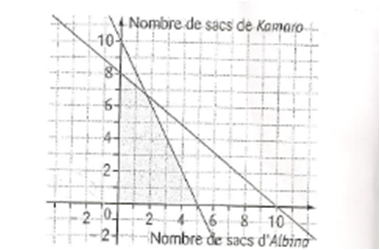
Le graphique (ci-dessous)représente le système (S). On admet que les couples de nombres entiers appartenant à la zone grisée répondent aux contraintes de volume et de masse du container.

1. lire graphiquement le nombre maximal de sacs de Kamaro que l'on peut charger avec un sac d'Albina.

2. Le sac de Kamaro est vendu 300 € et celui d'Albina 350 €. Déterminer la composition du chargement donnant la meilleure vente.

du container de volume 1m3 et de masse 400 kg.

[mtschoon]

Bonsoir,

Piste pour démarrer,

Partie A)

$1)a)200d{m}^3$=0.$2m^3$

réponse :0.2x

$1)b)210d{m}^3$=0.$1m^3$

réponse : 0.1y

2. En ajoutant :0.2x+0.1y ≤ 1

On peut améliorer cette inéquation en multipliant par 10 : 2x+y ≤10

3. pour x=2, l'inéquation précédente devient : 4+y ≤ 10

tu résous pour trouver y

Pour la partie B, tu utilises (pour les masses) une démarche totalement identique.