Résolution d'une équation différentielle

[AbAbsurdo]

Bonjour à tous,

Pour finaliser une étude dynamique (changement de vitesse d'un vélo) je dois résoudre l'équation suivante:

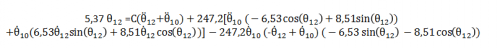
où C représente une constante (réelle)

Il me faut plus précisément exprimer ${\theta }_{12}$ en fonction de ${\dot{\theta }}_{10}$

J'ai pensé à passer en Laplace mais cela semble hors de ma portée (multiplication de cosinus par des dérivées secondes...).

Je sollicite donc votre aide, toute idée sera la bienvenue ^^

Merci d'avance

[AbAbsurdo]

J'ai réussi à simplifier mon équation !

$0,00000537\ast {\theta }_{12}(t)=2112,03\ast \frac{d^2{\theta }_{12}(t)}{d{t}^2}+1,18907289<em>10^5-8628.7632</em>cos({\theta }_{12}(t))+1,188542544\ast 10^5<em>sin({\theta }_{12}(t))+4,857993682</em>10^5\ast t^2<em>sin({\theta }_{12}(t))+6,691494523</em>10^6\ast t^2\ast cos({\theta }_{12}(t))$

Il me faut maintenant exprimer ${\theta }_{12}$ en fonction de t.

C'est toujours pas linéaire mais ça paraît plus simple

Pensez-vous par ailleurs qu'il faut forcément passer par une résolution numérique ?

Merci