Embouteillage et variable aléatoire
-
Bbrom2 dernière édition par
Bonjour, j'aimerais avoir de l'aide pour faire cet exercice :
Deux chaines d'embouteillage, la chaîne n°1 et celle n°2, remplissent des bouteilles d'eau et les emballent par 6, chaque pack de 6 bouteilles étant formé de bouteilles sortant toutes de la même chaine. 3/4 des bouteilles sortent de la chaine 1. On a constaté qu'1/10 bouteille sortant de la chaine 1 est mal remplie, respectivement 2/10 pour la chaine 2. On stocke ensemble tous les packs stockés et on note X la variable aléatoire égale au nombre de bouteilles mal remplies dans le pack choisi. Déterminer la loi de .
J'ai fait un arbre de probabilités, mais je ne pense pas que c'est ce qu'il faut ici .
Dans un pack, il peut y avoir au minimum 0 bouteille mal remplie et au maximum 6 bouteilles mal remplies.Loi suivie : loi binomiale B(6, ?)
je n'arrive pas à donner le succès étant donné qu'on a deux chaines à prendre en compte ?Merci de m'éclairer !
-
mtschoon dernière édition par

Bonjour,
Piste,
Ton idée d'arbre me parait bonne
Je te joins un début ( tu complètes, bien sûr , en calculant les probabilités)
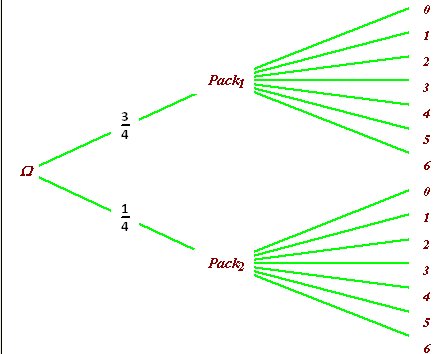
En appelant X1 le nombre de bouteilles mal remplies du Pack1 et X2 le nombre de bouteilles mal remplies du Pack2p(x=0)=34p(x1=0)+14p(x2=0) p(x=1)=34p(x1=1)+14p(x2=1)p(x=0)=\frac{3}{4}p(x_1=0)+\frac{1}{4}p(x_2=0) \ p(x=1)=\frac{3}{4}p(x_1=1)+\frac{1}{4}p(x_2=1)p(x=0)=43p(x1=0)+41p(x2=0) p(x=1)=43p(x1=1)+41p(x2=1)
.....
(Tu continues jusqu'à X=6)
-
Bbrom2 dernière édition par
merci.
Donc par exemple, pour p(X=0), on obtient :
p(X=0)=3/49/10+1/48/10 ?
La loi de probabilité est-ce une loi binomiale (j'en doute vu les calculs) ?
-
mtschoon dernière édition par

P(X=0) que tu viens de calculer n'est pas bon.
La loi de probabilité de X n'est pas binomiale mais La loi de probabilité de X1X_1X1 est binomiale et celle de X2X_2X2 aussi.
Prends le temps d'y réfléchir .
-
Bbrom2 dernière édition par
du coup, j'écrirai plutôt :
B1=(6,1/10) et B2=(6,2/10).
Donc :p(X=0)=3/4∗[6C0∗(9/10)p(X=0)=3/4*[6C0*(9/10)p(X=0)=3/4∗[6C0∗(9/10)^6]+1/4[6C0∗(8/10)6]+1/4[6C0*(8/10)^6]+1/4[6C0∗(8/10)6] par application des lois binomiales
-
mtschoon dernière édition par

oui.
-
Bbrom2 dernière édition par
ok merci je vais finir
-
mtschoon dernière édition par

Bons calculs.