Dénombrements (en vue des probabilités)
-
Sserenade dernière édition par
Une urne contient 10 boules numérotées de 0 à 9. On tire successivement et avec remise 4 boules de façon à former un nombre:
- commençant par zéro.
- se terminant par zéro.
- commençant par zéro et se terminant par zéro.
- commençant par zéro ou se terminant par zéro.
Je vous prie de bien vouloir m'expliquer cet exercice, car je ne comprends pas vraiment les probabilités.
Merci de votre compréhension.
-
Sserenade dernière édition par
Combien y'a-t-il de possibilités dans chaque cas?
-
mtschoon dernière édition par

Bonjour serenade,
Il s'agit de dénombrements.
Principe pour le 1)
Soit "abcd" un nombre à 4 chiffres.
Le nombre commence par 0 : 0 est la seule possibilité pour a, donc une seule possibilité pour a
pour b il y a 10 possibilités ( de 0 à 9)
ensuite, pour c il y a 10 possibilités ( de 0 à 9)
enfin,pour d il y a 10 possibilités ( de 0 à 9)
Le nombre total d'éventualités est donc : 1 x 10 x 10 x 10 =103=10^3=103=1000
Essaie te faire la même démarche pour les questions suivantes et donne nous tes réponses. Nous vérifierons.
-
Sserenade dernière édition par
Bjr mtschoon et merci de votre réponse
Donc pour2)
se terminant par zéro alors je considére que le nombre se termine par 0: il yaura une seule possibilité pour d.
Pour a 10 possibilité, pour b 10 possibilités, pour c 10 possibilité
le nombre total d'éventualité est donc: 10 x 10 x 10 x 1 = 10^3 = 1000
-
Sserenade dernière édition par
Pour la 3) on me dit: commençant par o et se terminant par 0
Donc si je comprends bien on fait l'intersection des deux premiers
Soit A l'ensemble des nombres commençant par 0 et B l'ensemble des nombres se terminant par 0
je dois faire A∩B n'est ce pas
-
mtschoon dernière édition par

Oui pour le 2)
Pour le 3), effectivement, c'est bien l'intersection dont il s'agit, mais il faut répondre à la question : nombre de possibilités.
Je te conseille de raisonner simplement ( même principe qu'au 1) et qu'au 2) ).
-
Sserenade dernière édition par
Pour le 3)
pour a: 1 seule possibilité
pour b: 10 possibilités
pour 10 possibilités
10 possibilités
pour d: 1 seule possibilitéDonc le nombre total d'éventualité est: 1 x 10 x 10 x 1 = 10^2 = 100
pour le 4)
je ne comprends pas, ou bien je dois passer par le cardinal des ensembles?
-
Sserenade dernière édition par
Est ce que je peux faire ceci
Pour 4)
Soit A l'ensemble des nombres commençant par 0 et B l'ensemble des nombres se terminant par 0Card(A∪B) = Card(A)+Card(B) - Card(A∩B)
Sachant que que Card (A∩B) = 100
On a : Card(A∪B) = 1000 +1000 - (100) = 1900
Donc le nombre total d'éventualités est: 1900
-
mtschoon dernière édition par

C'est bon pour la 3)
C'est bon aussi pour la 4)
Bravo !
-
Sserenade dernière édition par
Merci C'est Vous
-
Sserenade dernière édition par
S'il vous plaît s'il y a possibilité de faire un arbre est- ce-que vous pourriez m'expliquer le principe,(comment faire les branches à partir de cet exercice) si toutefois votre temps vous le permet.
Merci d'avance
-
mtschoon dernière édition par

Lorsque j'aurais un peu de temps, je te ferai un arbre, mais pas avec les valeurs de cet exercice !
J'espère que tu réalises que pour la question 1) par exemple, l'arbre aura 1000 branches...
-
mtschoon dernière édition par

Je t'indique comment faire un arbre relatif auxdénombrements.
Cela est commode pour comprendre le raisonnement, mais très mal commode dans la pratique car le nombre de branches devient vite très grand !Dans la suite de ton cours, lorsqu'il sera question de calculer des probabilités, tu verras, sur ce principe, un type d'arbre probabiliste pour lequel chaque chemin correspond à une probabilité et qui sera alors très commode.
J'adapte la question 1) avec des nombres plus petits.
Une urne contient 4 boules numérotées de 0 à 3. On tire successivement et avec remise 3 boules de façon à former un nombre.
Combien de possibilités pour obtenir un nombre commençant par zéro ?En raisonnant (comme au 1), la réponse est 1 x 4 x 4 =16
Si tu veuxillustrer cela par un arbre, chaque possibilité va correspondre à un chemin commençant au point nommé Ω et se terminant à chaque bout de branche.
Tu obtiens donc 16 chemins ( 000, 001, 002,003,010, 011, 012,013,020, 021, 022,023, 030, 031, 032,033 )
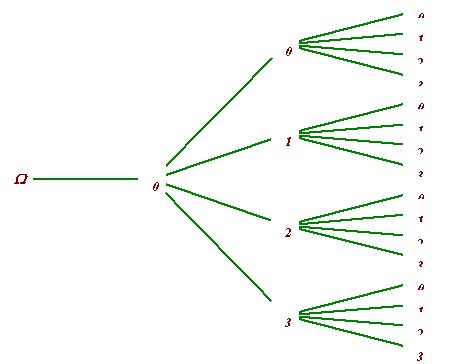
Je te laisse réfléchir et demande si tu ne comprends pas.
-
Sserenade dernière édition par
Bjr tout le monde
Bjr mtschoon et merci (l'arbre vous l'avez fait avec quel logiciel j'ai cherché hier à partir de Google)
j'ai l'ai bien regardé , et c'est vrai que quand il y'a plusieurs issues ça devient moins commode.
Mais si on avait:
Une urne contient 4 boules numérotées de 0 à 3. On tire successivement et avec remise 3 boules de façon à former un nombre.
Combien de possibilités pour obtenir un nombre se terminant par zéro ?
-
Sserenade dernière édition par
Est ce que l'arbre commencerai par le zéro devant?
-
mtschoon dernière édition par

L'utilitaire que j'ai utilisé est SineQuaNon, qui est gratuit et que tu peux télécharger.
L'arbre est l'illustration du raisonnement.
Si le nombre se terminait par 0 , le nombre de possibilités serait
4 x 4 x 1 =16
A partir du point de départ ( nommé Ω ), tu ferais 4 branches (0,1,2,3)
A l'extrémité de chacune de ces 4 branches , tu ferais 4 nouvelles branches (0,1,2,3)
A l'extrémité de chacune de ces 16 branches , tu ferais 1 nouvelle branche (0)