Les formules trigonométriques(compréhension)

Bonjour

Je voudrais comprendre les égalités suivantes:(explication)

cos(x) = cos(-x)
sin(x) = sin(-x)

Aide-moi s'il vous je ne comprends rien du tout sur les égalités trigonométriques
Merci de votre compréhension.....

Bonjour,

Il y a une erreur de signe dans la seconde égalité : sin(-x)=-sin(x)

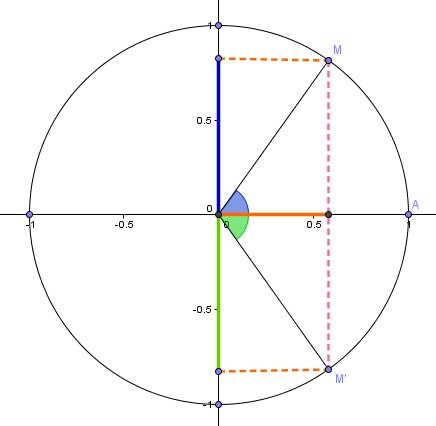
Je te joins un graphique du cercle trigonométrique pour t'aider à comprendre. $fichier math$

$\text{(\vec{OA},\vec{OM}) est l'angle dont une mesure est x (teinte bleue)$
$\text{(\vec{OA},\vec{OM'}) est l'angle dont une mesure est -x (teinte verte)$

M et M' sont symétriques par rapport à l'axe des abscisses.

L'abscisse de M est cos(x)
L'abscisse de M' est cos(-x)

Ces abscisses sont égales (trait continu rouge, sur l'axe des abscisses) , c'est à dire

$cos(-x)=cos(x)\fbox{cos(-x)=cos(x)}$

L'ordonnée de M est sin(x)
L'ordonnée de M' est sin(-x)

Ces ordonnées sont opposées (trait continu bleu et trait continu vert, sur l'axe des ordonnées) , c'est à dire

$sin(-x)=-sin(x)\fbox{sin(-x)=-sin(x)}$

J'espère t'avoir un peu éclairé.

Bonjour mtschoon

MERCI pour la figure et les explications et j'espère d'autres élèves comme moi en profiteront aussi.

Mais j'aimerais à partir de la figure aussi, que vous m'expliquiez d'autres égalités trigonométrique entre cos sin et tan leurs rapports trigonométriques...

Quand vous aurez un peu plus de temps s'il vous plaît...
Merci d'avance je suis ce topic

Merci infiniment pour tout ce que vous faîtes pour moi

Bonjour Serenade,

Les relations trigonométriques sont très nombreuses et j'ignore celles qui te sont vraiment utiles.

Je te mets un lien et te conseille de regarder les 3 premiers paragraphes seulement (jusqu'aux arcs associés).

Dans le premier paragraphe, la tangente est définie comme un quotient.
Lorsque j'aurais du temps, je t'indiquerai comment lire la tangente sur le cercle trigonométrique (sans passer par sinus et cosinus)

http://fr.wikiversity.org/wiki/Trigonométrie/Relations_trigonométriques#M.C3.A9thode_trigonom.C3.A9trique

Bon travail.

Merci
je vais de suite voir le lien.
Oui quand vous aurez le temps expliquez moi beaucoup plus amplement.

Bonjour,

Je t'indique comment lire la tangente sur le cercle trigonométrique (sans passer par sinus et cosinus)

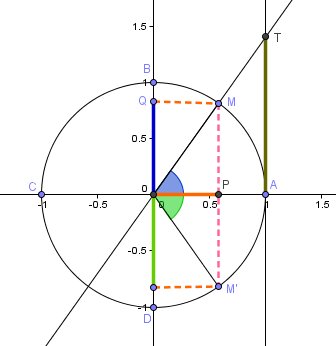
J'ai complété le schéma fait précédemment :

Axe appelé "axe des tangentes" : axe passant par A, parallèle à l'axe des ordonnées ("axe des sinus") et de même vecteur unitaire)

T point d'intersection de de cette axe avec la droite (OM)

tanx est l'ordonnée du point T dans le repère $(O,OA⃗,OB⃗)(O,\vec{OA},\vec{OB})$ , c'est à dire la mesure algébrique de (A,T).

On note :

$\text{tanx=\overline{AT}$

$fichier math$

Une explication :

$\text{tanx=\frac{sinx}{cosx}=\frac{\overline{OQ}}{\overline{OP}}=\frac{\overline{MP}}{\overline{OP}}=\frac{\overline{AT}}{\overline{OA}}$

Vu que$\text{ \overline{OA}=1$ ( rayon du cercle trigonométrique) :

$\fbox{\text{tanx=\overline{AT}}$

Pour être sûre d'avoir compris, lis par exemple :

$\text{tan (\frac{\pi}{4})$

$\text{tan (\frac{-\pi}{4})$

Bonjour
Merci mtschoon