Montrer des égalités à l'aide du théorème de Thalès

Bonjour,

J'ai un souci avec la question c) de l'exercice suivant :

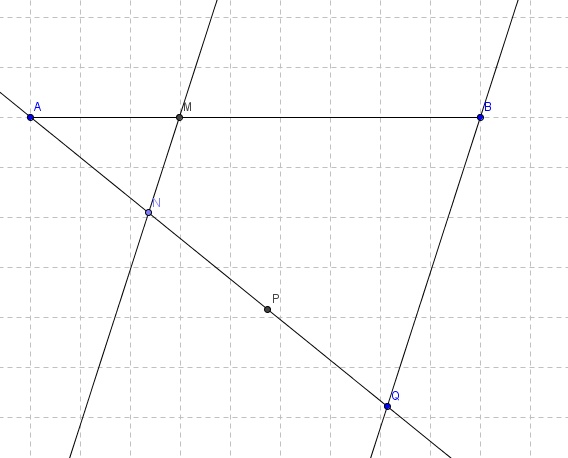
a) Sur une feuille blanche, tracer un segment [AB] de longueur quelconque (la longueur AB restera inconnue car la construction à réaliser ne nécessite pas cette information).

On cherche à placer, sans calculs, un point M sur la droite (AB) tel que AM/AB=1/3

La méthode ci-après permet de l'obtenir.
On demande de réaliser cette construction, étape par étape, à partir du segment [AB] précédent et de laisser visible tous les traits de constructions.

*Tracer un demi-droite d'origine A, distincte de [AB)

Sur cette demi-droite, placer à l'aide d'un compas trois points distincts N, P et Q tels que AN=NP=PQ
-Tracer la droite (QB)
*A l'aide du compas construire la parrallèle à (QB) passant par N, elle coupe la droite (AB) en M.

b) Démontrer que le point M ainsi construit répond bien à la question, c'est-à-dire que AM/AB=1/3

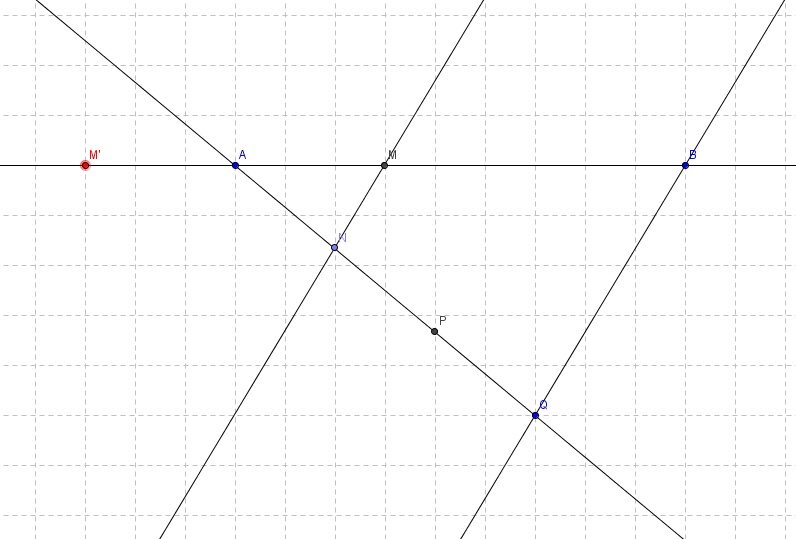
c) Existe-t-il un autre point M qui réponde à la question ? Si oui, comment l'obtenir ? Placer sur la figure le point M' correspondant à ce second emplacement.

Pour la question b)
théorème de Thalès :
AM/AB=AN/AQ=MN/BQ

De plus, on sait que AN=NP=PQ et ANPQ sont alignés
donc AQ=3xAN

AN/AQ=AN/(3xAN)=1/3

Or AN/AQ=AM/AB

D'où AM/AB=1/3
CQFD

Et là, je bloque pour la question c).
Quelqu'un peut-il m'aider ?
Merci !!!

Bonjour,
Montre le figure obtenue.

Voici la figure que j'obtiens :

Bien.
Pour la question c :
On a AM/AB = 1/3
On souhaite AM'/AB = 1/3
Donc on veut que AM' = AM
Alors, où placer le point M' ?

Effectivement, on veut que AM=AM' tout en conservant l'égalité de Thalès.
Du coup, soit, M et M' sont confondus (aucun intérêt), soit N et M' sont confondus. (?)
A part ça, je ne vois pas où le placer...

Sur la droite (AB) tu as déjà le point M.
Tu veux aussi placer M' sur cette droite de façon que AM' = AM.
Je parle bien de la droite (AB), pas du segment.
Tu ne vois pas ce qu'on peut dire de M' ?

Du coup, je ne vois que ça !

Et donc, AM'/AB=1/3
car AM'=AM

Est-ce correct ?

Ton dessin avec M' est correct, mais ton raisonnement "tourne en rond".
C'est parce qu'on veut que AM'/AB = 1/3 , comme AM/AB, que AM' = AM.
Comment sont M et M' ?

M et M' sont symétriques, par rapport à A.
Mais je ne vois pas où tu veux en venir...

Citation
c) Existe-t-il un autre point M qui réponde à la question ? Si oui, comment l'obtenir ? Placer sur la figure le point M' correspondant à ce second emplacement.
C'est la réponse à cette question, tout simplement.

Ah ok !
Je cherchais compliqué !!!

Merci pour ton aide et le temps que tu m'as accordé.
Bonne fin d'après midi.

De rien, mais encore une chose : je n'avais pas bien lu ta réponse à la question b).
Tu écris
Citation
AN/AQ=AN/(3xAQ)=1/3
ce qui est évidemment contradictoire : AN/AQ = 1/3 parce que AQ = 3.AN.
Tu feras attention en rédigeant.

Oui, autant pour moi. Erreur de frappe sur le clavier.
Je vais corriger les messages plus haut pour éviter que d'autres fassent une erreur en recopiant.
Merci !

De rien.