Trouver les ensembles représentant les intervalles d'intersection

Bonjour,

Voici le tabelau que je doit remplir, j'ai commencé à mettre les ensembles mais ensuite je bloque.
Merci de bien vouloir m'aider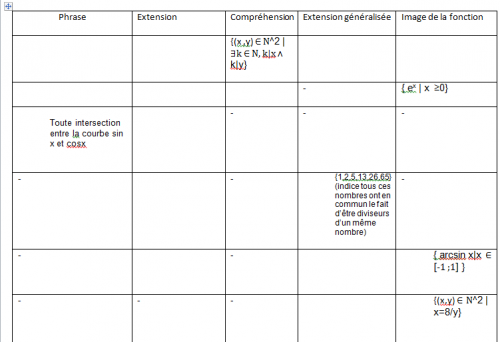

le tableau

Bonjour,

Je t'indique seulement quelques pistes relatives à chaque ligne écrite.
Complète à ta guise (c'est TON travail)

1ere ligne :
Pour tout couple (x,y) de N², on peut prendre k=1 car 1|x et 1|y
Tout couple (x,y) de N² satisfait à la condition indiquée

2eme ligne :
Etudie les variations de x-> $e^x$ pour x ≥ 0
Tu dois trouver l'intervalle [1,+∞[

3eme ligne :
Si l'on ne parle que des abscisses des points d'intersection :
sinx=cosx <=> x=pi/2+k∏, k ∈ Z <=> x ∈ {..., (pi/2)-2∏,(pi/2)-∏,pi/2,(pi/2)+∏,(pi/2)+2∏,....}

4ème ligne :
Je ne comprends pas ce que fait l'écriture dans la colonne "Extension généralisée"... c'est plutôt une "Extension".
Regarde les nombres écrits et leur décomposition en facteurs premiers.
26 = 2 x 13 et 65 = 5 x 13
2 x 5 x 13 = 130
Si tu cherches l'ensemble des diviseurs de 130, tu dois trouver {1,2,5,10,13,26,65,130}
L'ensemble indiqué est donc l'ensemble de diviseurs de 130 privé de 10 et 130 (c'est à dire privé des multiples de 10)

5eme ligne :
Etudie les variations de x-> arcsinx pour x ∈ [-1,1]
Tu dois trouver l'intervalle[-∏/2,∏/2]

6eme ligne:
Nécessairement x et y sont non nuls.
8 = 2 x 4
Tu dois trouver les couples (1,8),(8,1), (2,4) et (4,2)

Vérifie toutes mes pistes car j'ai fait vite.

Bon courage pour cet exercice.

D'accord merci

Que veux dire ce signe -∏

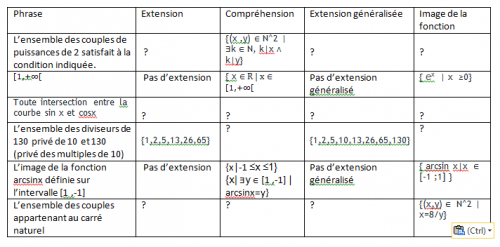
Voila ce que j'ai fait, merci de me corrigé, les ? veut dire que je ne sais pas

$fichier math$

∏=Pi=3,14............

Dac, peux tu me dire si la ligne 2 est correct ?

Pour la ligne 2, j'ignore ce qui est attendu, mais tes réponses sont cohérentes.

Dac pour la ligne 3 peux tu m'aider

Je t'ai donné des idées (à creuser) pour chacune des lignes...

Relis mon premier post .

Oui mais je trouve l'exercice trop élevé par rapport à mon niveau, donc je ne sais pas faire

Commençons par la ligne 1:
k=1 car 1|x et 1|y Je peux mettre en extension généralisé ou extension ?

Pour la ligne 3 : je propose en compréhension : x=pi/2+k∏,
En extension généralisé k ∈ Z <=> x ∈ {..., (pi/2)-2∏,(pi/2)-∏,pi/2,(pi/2)+∏,(pi/2)+2∏,....}
En extension: je sais pas
Image de la fonction sinx=cosx

Comme je te l'ai déjà dit deux fois,tu as l'aide mathématique dans ma première réponse.
Il faut ensuite que tu approfondisses ton cours, pour savoir exactement les définitions précises des termes employés pour pouvoir compléter le tableau. Je n'ai pas ton cours...donc je ne peux pas te donner des détails.

Pour la ligne 1, je me demande bien ce que tu a voulu écrire..."L'ensemble des couples de puissance de 2" ! ! ! ...cela n'a aucun sens.

Ne fais que ce que tu comprends.

Vu que la propriété indiquée est toujours vraie; il s'agit de N²=N x N .
N² est l'ensemble des couples (x,y) de deux naturels.

$\text{n^2={(x,y) | x\in n \wedge y\in n}$

En extension généralisée ( vu qu'il y a une infinité de couples)

$n^2=\text{{(0,0),(0.1),(0,2)...,(1,0),(1,1),(1,2),...,...}$

Pour la ligne 3, n'oublie pas k ∈ Z , sinon c'est faux

Vu qu'il y a une infinité d'éléments, il s'agit d'une extension généralisée.

sinx=cosx n'est pas une fonction ; c'est une équation.

Tu peux revoir aussi les lignes suivantes.