Preuves par récurrence

Bonsoir, merci de bien vouloir m'aider :

Prouver par récurrence :

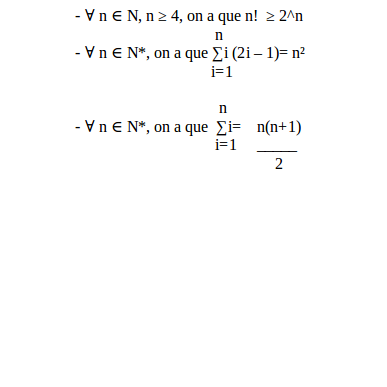
$fichier math$

Titre complété

Bonjour,

Merci de nous indiquer ce que tu as commencé à faire.

Remarque : la seconde formule écrite me laisse perplexe..( fais une vérification, par exemple pour n=2 ...). Une faute de frappe peut-être ?

Pour la 2) il y a une erreur de frappe, donc avant (2i-1) il n'y a pas i.

je n'ai jamais fais de preuve par recurrence

C'est bien ça la faute d'énoncé du 2)

Si tu n'a pas de cours (?) et si tu n'as jamais vu le raisonnement par récurrence (?), il faut commencer par comprendre la méthode avant de faire des exercices.

Eventuellement, regarde ici :

http://www.mathforu.com/cours-113.html

Lorsque tu as compris le principe, essaie de faire la première question et indique nous ce que tu as trouvé.

Bon j'ai reussi a faire le 3ème, tu peux me montrer pour la première stp

je viens de réussir pour le premier

je n'arrive pas pour la deuxième

Pour la 2) : Même principe que pour la 3)...

Initialisation

$\bigsum_{i=1}^1(2i-1)=2-1=1$

$1^2=1$

donc..................

Hérédité

Hypothèse:
à un rang n( n≥4) ( tu peux mettre "p" au lieu de "n", si tu préfères)

$\bigsum_{i=1}^n(2i-1)=n^2$

Conclusion à démontrerau rang (n+1):

$\bigsum_{i=1}^{n+1}(2i-1)=(n+1)^2$

DEMONSTRATION (piste)

$\bigsum_{i=1}^{n+1}(2i-1)= \bigsum_{i=1}^n(2i-1)+2(n+1)-1=n^2+2(n+1)-1$

Tu termines le calcul et tu dois trouver (n+1)²

Conclusion générale

La propriété est vraie à l'ordre 1 et elle est héréditaire à partir de n=1, donc elle est vraie pour tout n supérieur ou égal à 1.

D'accord merci de ton aide

De rien .* J'espère que tu as compris.*