Déterminer si deux droites sont parallèles

les longueurs sont exprimées dans la même unité .
les droites ( AB ) et ( CD ) sont elles parallèles ?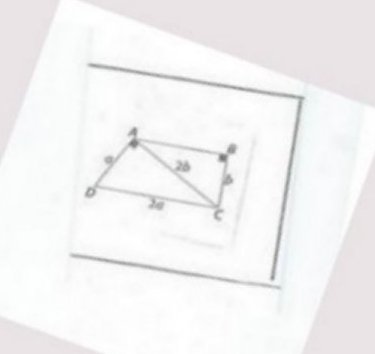

$fichier math$

*(Bien que guère nette, je viens de retourner ton image pour pouvoir lire à peu près correctement)
*

Bonjour !

Ici, on dit "Bonjour" lorsqu'on vient demander de l'aide...

Une autre fois, mets la figure dans le bon sens pour pouvoir mieux lire.

Piste,

Dans le triangle rectangle ABC, tu peux calculer le cosinus de l'angle (BCA)

$cos⁡(bca^)=bcac=...=12\cos(\widehat{bca})=\frac{bc}{ac}=...=\frac{1}{2}$

Donc,

$bca^=60degres\widehat{bca}=60 degres$

Dans le triangle rectangle ADC, tu peux calculer le sinus de l'angle (ACD) et tu pourras déduire que :

$acd^=30degres\widehat{acd}=30 degres$

Tu pourras ainsi trouver la valeur de l'angle $bcd^\widehat{bcd }$ et tirer la conclusion.

si je conclus bien les droites ne sont pas parallèles

Tu te trompes...

J'espère que tu as bien trouvé que l'angle(BCD) vaut 90°.

$\text{les angles \widehat {abc} et {\widehat {bcd} sont droits, donc ...$

ah non je n ai pas trouvé 90 °

Revois ma première piste tranquillement...

60°+30°=90° donc...

pffff je ne trouve pas

Bien sûr, il faut que tu connaisses ton cours de trigonométrie (angles de 30°,60°)

$cos⁡(bca^)=bcac=b2b=12\cos(\widehat{bca})=\frac{bc}{ac}=\frac{b}{2b}=\frac{1}{2}$

donc

$bca^=60degres\widehat{bca}=60 degres$

$sin⁡(acd^)=adcd=a2a=12\sin(\widehat{acd})=\frac{ad}{cd}=\frac{a}{2a}=\frac{1}{2}$

donc

$acd^=30degres\widehat{acd}=30 degres$

$dcb^=acd^+bca^=30degres+60degres=90degres\widehat{dcb}=\widehat{acd}+\widehat{bca}=30 degres+60 degres=90 degres$

Tu tires la conclusion.

merci

De rien !