transformation du graphe d'une fonction
-
Mmomona dernière édition par
Bonsoir, juste une petite question toute bete mais j'ai pas envie d'avoir d'ambiguïté...
On donne le domaine graphe d'une fonction f définie sur (-10;6)
- Déterminer le domaine de définition puis tracer le graphe Cg de la fonction g(x)= f(2x) - 3
Donc ca ok pas de probleme. Grace aux coordonées des points de Cf j'ai deduits les coordonées de Cu grace à une fonction u definie sur (-5;3) par u(x)= f(2x)
Puis j'en ai deduits les coordonnées des points de Cg grace a la fonction g définie sur (-5;3) par g(x)= f(2x) - 3Mais maintenant je dois reprendre avec le même enoncé pour la fonction h(x)= f(2x-3)
Du coup j'ai dis que h(x) existe si et seulement si f(2x-3) existe
c'est a dire : 2x-3 ∈ Df
-10< 2x-3 < 6
-7/2< x < 9/2Mais du coup pour deduire les coordonnées avec la meme methode qu'avant je sais pas trop si il faut que je prenne d'abord une fonction v(x)= f(2x) avec Dv= ( -5; 3) puis la fonction h(x)= f(2x-3) avec Dh = ( -2; 6)
Ou alors commencer avec la fonction v(x)= f(x - 3/2 ) avec Dv= ( -8,5 ; 7,5 ) puis avec h(x)=f(2x-3) avec Dh= ( -7/2 ; 9/2 )
Une petite aide est la bienvenue ... Merci

-
mtschoon dernière édition par

Bonjour,
Pour les transformations, tu peux regarder ici :
http://www.parfenoff.org/pdf/1re_STI2D/analyse/1re_STI2D_Fonctions_%20associees_a_fonction_u.pdf
-
Mmomona dernière édition par
Ok j'ai regardé mais je suis toujours pas sur de moi ...

-
mtschoon dernière édition par

Il y a plusieurs façons de voir la chose.
Ta dernière idée f(2x−3)=f(2(x−32))f(2x-3)=f(2(x-\frac{3}{2}))f(2x−3)=f(2(x−23)) est bonne.
Pour clarifier, je l'ai réalisée avec f(x)=x2f(x)=x^2f(x)=x2
(sans tenir compte de l'ensemble de définition, seulement pour le mécanisme de composition)
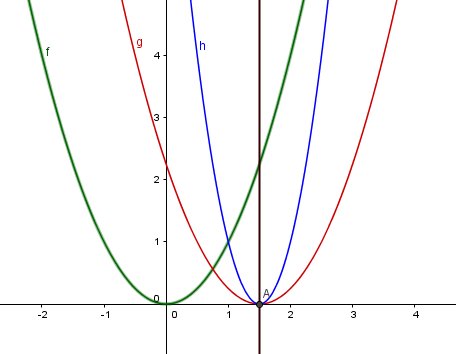
(Cf) courbe d'équation y=f(x) en vert
(Cg) courbe d'équation y=f( x- 3/2 ) en rouge
(Ch) courbe d'équation y=f(2(x- 3/2 )) en bleuOn passe de (Cf) à (Cg) partranslation horizontale de vecteurv⃗=32i⃗\vec{v}=\frac{3}{2}\vec{i}v=23i
On passe de (Cg) à (Ch) par compression horizontalepar un facteur de 2