Montrer qu'une fonction est continue en...
-
NNayaa dernière édition par
Bonjour à tous et toutes,
Alors voilà, j'ai repris des études en bio-ingénierie à l'université (je suis belge) mais cela fait 5 ans que je n'ai plus fait de maths (j'ai travaillé entre-temps). Autant dire que je suis perdue dans ce cours depuis la reprise...
Nous avons ici un devoir à rendre vendredi et il ne m'a pas l'air difficile du tout, mais je n'arrive pas à démarrer. Je me demandais si vous pouviez m'éclairer quant à la démarche à suivre pour résoudre cette question, histoire que je sache comment m'y prendre et quelle(s) question(s) me poser. J'éprouve également des difficultés avec les notations mathématiques (qui recouvrent chaque page de mon syllabus), donc si vous pouviez être patients avec moi, ce serait gentil.

Voici l'énoncé :
"Montrer que la fonction f: R-->R définie par :f(x) = { √x²-2x+2 -1 (si x≠1) et (normalement sur une seconde ligne dans l’accolade) 1/2 (si x=1)
est continue en 1."
Pour la première équation, le "-1" n'est pas compris dans la racine apparemment.
Voilà, comment puis-je commencer cet exercice et comment montrer qu'elle est bien continue en 1 ? Quand je vois la première équation, j'ai dans le souvenir le delta etc, mais mon dieu c'est vraiment loin et je ne sais pas si je suis dans le bon. Une fois que je me serai remise dans tout ça, je pense que ça ira mieux, mais il faut que je me remette en mémoire beaucoup de notions qu'on a tendance à vite oublier en sortant de l'école... et je ne me doutais pas que je reprendrais des études scientifiques un jour.

Je pense avoir bien compris ce qu'était une fonction continue (mais avec les notations, j'ai plus de mal à m'y retrouver quand il faut assembler le tout), mais je ne vois pas comment prouver qu'une fonction est continue (ici en 1 donc).
-
mtschoon dernière édition par

Bonjour,
Dans tout ce que tu as écrit, je crois lire que :
$\left{ f(x)=\sqrt{x^2-2x+2}-1\ pour\ x\ne 1\f(x)=\frac{1}{2} \ pour \ x=1\right$
Pour démontrer la continuité de f en 1, il faudrait prouver que :
$\fbox{\lim_{x\to 1} f(x)=f(1)}$
c'est à dire que :
limx→1f(x)=12\lim_{x\to 1} f(x)=\frac{1}{2}limx→1f(x)=21
Il faudrait que tu revois cet énoncé car avec l'expression de f(x) donnée :
limx→1f(x)=0\lim_{x\to 1} f(x)=0limx→1f(x)=0
La fonction f que tu donnes n'est pas continue en 1
-
NNayaa dernière édition par
Bonjour,
Merci beaucoup pour la réponse ! Je l'ai lue mais j'y regarderai plus en profondeur ce soir car je dois me rendre en cours et je rentre tard malheureusement.
Je suppose qu'elle peut éventuellement ne pas être continue en 1, je me renseignerai auprès de mes camarades si c'est possible. On ne peut pas joindre un fichier photo ici ?
Mais par contre je ne vois pas ce que je peux faire avec la première fonction. x ne doit pas valoir 1 dans le premier cas, c'est ça ?
Ce sont des choses que je me souviens avoir vues et que je maîtrisais à l'époque mais aujourd'hui ça me semble vraiment flou, c'est vraiment chiant.

-
mtschoon dernière édition par

La fonction f est définie en deux cas distincts :
1er cas x≠1: cela te permet de calculer f(x) pour toute valeur de ]-∞,1[ U ]1,+∞[
Tu peux ainsi faire tendre x vers 1 (c'est à dire donner à x des valeurs de plus en plus proches de 1)2ème cas : x=1 : cela te permet de calculer f(1)
Rappel : si l'énoncé que tu donnes est bon, f n'est pas continue en 1
PS : ici, les énoncés doivent être écrits à la main.
Tu peux insérer une image seulement s'il s'agit d'un graphique sans texte.
-
NNayaa dernière édition par
Rah je me suis trompée en fait dans l'écriture de la première fonction, c'est bien comme tu l'as écrit (√x²-2x+2 -1 (-1 hors racine) mais sur (x-1)² (et donc si x≠1)). Je ne pense pas que ça change grand-chose pour mon problème mais sait-on jamais...
C'est donc une division de fonctions continues, mais le souci provient donc toujours du 1/2, c'est bien ça ?
Je repasse demain matin pour écrire ce que j'ai obtenu.

-
mtschoon dernière édition par

Mais, ça change tout ! ! !
$\left{f(x)=\frac{\sqrt{x^2-2x+2}-1}{(x-1)^2} \ pour \ x\ne 1\f(x)=\frac{1}{2}\ pour\ x=1\right$
Tu dois trouver que :
$\fbox{\lim_{x\to 1}f(x)=\frac{1}{2}}$
donc :
$\fbox{\lim_{x\to 1}f(x)=f(1)}$
donc
f continue en 1
-
NNayaa dernière édition par
Zut, mille excuses !
Mais du coup je bloque pour ce que je dois calculer sous la racine. Je ne peux pas avoir un nombre négatif sous la racine, mais avec la technique du delta je tombe justement sur un nombre négatif (et avec un nombre négatif pour delta, pas de solution, c'est bien ça ?). Comment ça se passe dans ce cas-là ? Je ne sais pas si j'utilise la bonne technique mais je regarde quelques vidéos et il me semble normal d'employer celle-ci, sinon je ne vois pas trop, mais comme je patauge je me trompe sûrement.
Je me sens vraiment archi-nulle.
-
mtschoon dernière édition par

Il faudra simplement que tu revois tes bases.
Il n'y a pas de problèmes d'existence de f, f est définie sur R
Sous la racine, comme tu dis, le polynôme du second degré a un discriminant strictement négatif ; il est toujours du signe de "a" donc toujours strictement positif.
Le problème posé est de trouver la limite de f(x) lorsque x tend vers 1.
Y es-tu arrivé(e) ?
-
NNayaa dernière édition par
Alors voici ce que j'ai obtenu :
J'ai fait 2 factorisations pour la première équation
- La première : A² - B² avec :
$\ \ \frac{\sqrt{x^2-2x+2}-1}{(x-1)^2} \times \frac{\sqrt{x^2-2x+2}+1}{\sqrt{x^2-2x+2}+1} \ \ \$
- La seconde pour le (x-1)² que j'ai obtenu au dénominateur (A² - 2AB + B²), et j'ai pu annuler le numérateur et une partie du dénominateur.
Il me restait :
$\ \ \frac{1}{\sqrt{x^2-2x+2}+1} \ \ \$
Et là j'ai remplacé les x par 1 et j'ai obtenu 1/2 mais je ne sais pas si c'est correct, j'avais fait ça un peu parce que je cherchais une solution mais j'ai essayé plusieurs choses (en fait je suis perturbée par le x≠1 dans la première équation de l'énoncé).
-
mtschoon dernière édition par

Pour x≠1 (1er cas) , ta transformation de f(x) est bonne , mais bien sûr, il ne faut pas l'appliquer pour x=1.
Pour x≠1,tu peux faire tendre x vers 1:
x²-2x+2 tend vers 1
f(x) tend vers 1/2
Comme 1/2 est la valeur de f(1) ( deuxième cas), la fonction f est bien continue en 1
-
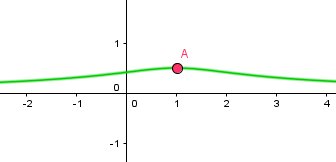
mtschoon dernière édition par

Pour t'éclairer , je te mets le graphique ( en vert le 1er cas, en rouge le 2ème cas).
Je pense que la notion de continuité en 1 saute aux yeux.