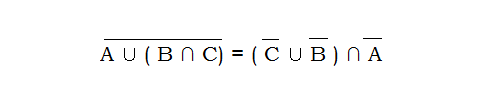Valeurs de vérité-Diagramme de Venn

Bonjour à toutes et à tous,

Voilà j'ai deux exercices à faire je pense avoir réussi le premier exercice, mais le deuxième je suis bloqué.

Ensuite, prouver en employant un tableau d’appartenance que si A,B,C sont des ensembles + voir image pour le reste de l'énoncer.

Je ne comprends pas du tout l'exercice, qu'est-ce que c'est un tableau d'appartenance ? Puis, le reste je ne comprends pas du tout...

Je vous suis très reconnaissant pour votre aide.

Merci d'ouvrir une autre discussion, si besoin, pour ton exercice 1.

Bonjour,

Remarque : ici, on ne met qu'une exercice par topic (car c'est impossible de répondre clairement à deux questions à la fois)

J*e te réponds à la question 2, vu que tu bloques sur celle là.
(Si tu as besoin de complément pour la question 1, ouvre un autre topic)
*

2.Je pense que le "tableau d'appartenance" dont tu parles s'appelle parfois "tableau de vérité"

Vu que tu as 3 parties A, B, C, tu as 11 colonnes à prévoir

$\text{x\in a | x\in b | x\in c | x\in (b\cap c) | x\in a\cup (b \cap c) | x\in \overline{(a\cup (b\cap c)}$

$\text{x\in \overline{a} | x\in \overline{b} | x\in \overline{c} | x\in \overline{c}\cup \overline{b} | x\in (\overline{c}\cup \overline{b})\cap\overline{a} |$

Tu écris les titres des 11 colonnes sur une seule ligne (j'ai fait un retour à la ligne, faute de place...)

Pour les valeurs de vérité, tu mets des 0 et de 1 ou des F et des V, selon tes habitudes
FAUX se traduit par F ou 0
VRAI se traduit par V ou 1
Tu peux aussi sous-entendre "x ∈" est ne mettre que le nom de la partie.

Pour x∈A, x∈B, x∈C tu commences par mettre les 8 possibilités :

0 0 0
0 0 1
0 1 0
1 0 0
1 1 0
1 0 1
0 1 1
1 1 1

Lorsque ton tableau est constitué, il te faut remplir toutes les cases vides par logique en utilisant les propriétés de l'union, intersection et complémentaire.

Le but : obtenir les mêmes valeurs de vérité pour les colonnes $x∈(a∪(b∩c)‾x\in \overline{(a\cup (b\cap c)}$ et $x∈(c‾∪b‾)∩a‾x\in (\overline{c}\cup \overline{b})\cap\overline{a}$

Reposte si tu n'as pas compris mon explication car faute de place pour composer le tableau, ce n'est pas facile...

Pour t'aider à comprendre, je te mets un lien ici :

http://www.grappa.univ-lille3.fr/~torre/Enseignement/Cours/logique.php

Les exemples sont relatifs à deux parties A et B, mais le principe est le même pour trois (à part que c'est beaucoup plus lourd à gérer ...)

Bonsoir Mtschoon,

Ah excusez-moi d'avoir mis 2 exercices... Effectivement le deuxième exercice me pose beaucoup de problème, et je te remercie pour ton aide.

Maintenant je ne sais pas combien de ligne faut-il ajouter ? Et pourquoi ?

Pour la première colonne x ∈ A quelle est le raisonnement à suivre ? Comment savoir si c'est vrai ou faux , comment l'expliquer ?

Une table d'appartenance est une table de vérité merci je ne savais pas merci

Bonne soirée

(Ton long tableau pose quelques problèmes à l'écran...)

Ta disposition en mettant les deux parties à comparer entre elles en bout de ligne, est très bien.

Pour les lignes à mettre en dessous : il y en a 8 (car $8=2^3$ )

EXPLICATION :

Tu as 3 propositions : x∈A, x∈B, x ∈C
Elles ont chacune2 valeurs de vérité ( Vrai ou Faux)
Bilans : 2 possibilités pour x∈A suivies de 2 possibilités pour x∈B suivies de 2 possibilités pour x∈C
(tu peux faire un arbre pour comprendre).

Bilan : 2 x 2 x $2=2^3$ =8

Je t'ai déjà indiqué ce que tu dois mettre dans les 3 premières cases (x∈A, x∈B, x ∈C) de ces 8 lignes:

0 0 0
0 0 1
0 1 0
1 0 0
1 1 0
1 0 1
0 1 1
1 1 1

La 1ere ligne correspond à x n'appartient ni à A, ni à B , ni à A
La 2eme ligne correspond à x appartient seulement à C
La 3eme ligne correspond à x appartient seulement à B
La 4eme ligne correspond à x appartient seulement à A
La 5eme ligne correspond à x appartient seulement à A et à B
La 6eme ligne correspond à x appartient seulement à A et à C
La 7eme ligne correspond à x appartient seulement à B et à C
La 8eme ligne correspond à x appartient à la fois à A , à B , à C

Pour mieux comprendre, tu peux faire le diagramme de Venn avec un ensemble E et 3 parties A, B,C
Tu trouveras les 8 positions possibles d'un élément x de l'ensemble E.

Ensuite, ton travail pourra commencer pour remplir logiquement toutes les cases vides.

Bonsoir,

Merci pour toutes tes explications je commence à comprendre de mieux en mieux grâce à toi, je vais essayé de compléter le tableau maintenant.

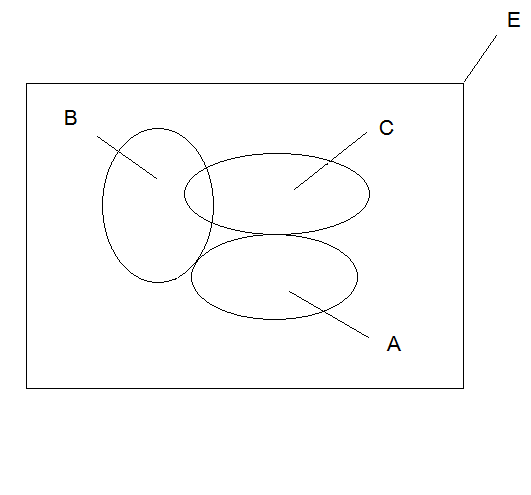
Par contre au niveau du diagramme de Venn j'ai essayé de le faire voici ce que ça donne je ne sais pas si c'est correcte surtout pour l'ensemble A ? Les parenthèses me perturbent...

Je rappel que c'est pour cet exercice

Bonne soirée

Comme tu me l'as signalé, j'ai fait des alternances dans les notations que je viens de rectifier. Merci de l'avoir vu.

Ce que tu as fait dans ta précédente réponse est bon (je l'ai supprimé car sa "grande largeur" perturbait totalement mon écran...)

Pour le diagramme de Venn, ton schéma est un cas particulier car A,B,C ont une intersection vide ainsi que B et C, et C et A.
Tu ne peux donc pas "voir" ainsi les 8 positions possibles de x.

Je te mets un schéma.

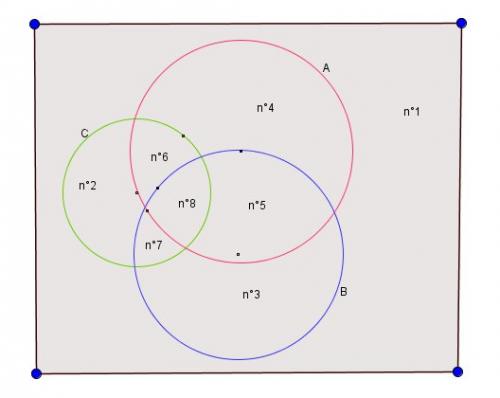
$fichier math$

Légende :
E est l'intérieur du rectangle
A est l'intérieur du cercle rouge
B est l'intérieur du cercle bleu
C est l'intérieur du cercle vert

Les numéros correspondent à la liste précédemment ndiquée :
0 0 0 : n°1
0 0 1 : n°2
0 1 0 : n°3
1 0 0 : n°4
1 1 0 : n°5
1 0 1 : n°6
0 1 1 : n°7
1 1 1 : n°8

Bonsoir Mtschoon

Merci pour ton schéma, c'est vraiment super bien expliqué, demain je vais essayé de recommencer l'exercice à zéro.
Normalement je pense pouvoir y arriver, mais si tu as le temps ça serait sympa que tu y jettes un oeil 2 minutes si ça ne te dérange pas, pour voir si je suis pas à côté de la plaque...

Bonne soirée

Cela ne me gène pas du tout mais vu la largeur du tableau, décompose le tableau en deux parties.
Peut-être aussi que tu n'auras aucune difficulté pour remplir les case vides.

Bonne journée !

Bonsoir Mtschoon,

J'ai complété le tableau pour les 7 premières colonnes, (ils sont assez facile) que penses-tu ? Je ferais les 4 autres après ta correction...

Pour agrandir le tableau, il faut juste cliquez sur l'image.

Merci encore

Quelques erreurs

Raisonne logiquement.

Dans les colonnes des complémentaires , il doit y avoir 0 au complémentaire lorsqu'il y a 1 à la partie et 1 au complémentaire lorsqu'il y a 0 à la partie

Pour l'intersection de 2 parties, il doit y avoir 1 à l'intersection lorsqu'il y a 1 à chacune des 2 parties.
Dans les autres cas, il y a 0 à l'intersection.

Bonsoir Mtschoon,

Merci pour ta correction, je pense que maintenant ça doit être juste ?

La première partie du tableau est juste.

Il y a des erreurs dans la seconde partie (celle du dessous)

Pour l'union de 2 parties, il doit y avoir 1 à l'union lorsqu'il y a au moins un 1 à l'une des 2 parties (c'est à dire 1,0 ou 0,1 ou 1,1)
Dans l'autre cas (c'est à dire 0,0), il y a 0 à l'union.

Pour t'éviter peut-être de refaire une nouvelle image, je t'indique ce que tu dois trouver dans les deux dernières colonnes du second tableau

1 1
1 1
1 1
0 0
0 0
0 0
0 0
0 0

Bien sûr, redonne ton second tableau si tu as un doute sur tes réponses.

Bonsoir Mtschoon,

Les 4 dernières colonnes me pose plus de problème que la première partie, normalement ça doit être bon exacte maintenant...

En tout cas merci pour tes réponses.

Cela n'a pas d'influence sur le résultat final, mais je crois voir deux erreurs pour $\in \overline{c} \cup \overline{b}$ (tu n'as trouvé que des 1, il me semble, vérifie)

Pour $\in \overline{c} \cup \overline{b}$ , tu devrais trouver :

1
1
1
1
1
1
0
0

Fais une vérification générale (on ne sait jamais...) et tout devrait être bon.

Bon travail.

Merci beaucoup Mtschoon pour ton aide.

De rien

Bon travail !

Bonsoir Mtschoon,

J'aurai bien voulu savoir ce que tu avais pour

Voici mes réponses:
0
0
0
1
1
1
1
1

Je pense que c'est correcte, mais je préfère te demander.

Bonne soirée

C'est bien ça.

Bonne soirée à toi.

Merci

Bon travail !