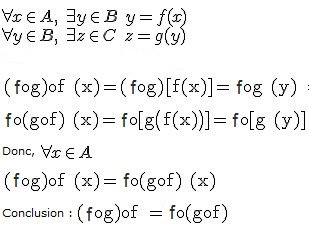Associativité de la loi o
-
AAugustin1340 dernière édition par
Bonsoir,
J'aurais besoin d'une petite explication:
Si 3 ensembles, A,B,C sont en réalité un seul et même ensemble, est-ce que
fo(gof) = (fog) of ?Je me souviens que le prof a parlé de ça, il y a 2 semaines en mettant un exemple,
(voir photo,) mais je ne m'y retrouve pas trop dans mes notes. Nous n'avons pas de syllabus et le prof fonce à chaque cours, et j'aimerais bien comprendre cette exercice pour ne pas prendre du retard.Merci pour votre aide.
-
mtschoon dernière édition par

Bonsoir,
Il s'agit de la propriété d'associativité de la loi o, c'est à dire prouver que (hog)of=ho(gof)
Je trouve l'explication donnée rapide mais claire.
Je tenterai de te l'expliciter davantage si besoin.
-
mtschoon dernière édition par

Bonjour,
Soit A, B, C, D les ensembles
∀x∈a, ∃y∈b y=f(x)\forall x \in a, \ \exists y \in b \ y=f(x)∀x∈a, ∃y∈b y=f(x)
∀y∈b, ∃z∈c z=g(y)\forall y \in b, \ \exists z \in c \ z=g(y)∀y∈b, ∃z∈c z=g(y)
∀z∈c, ∃y∈d t=h(z)\forall z \in c, \ \exists y \in d \ t=h(z)∀z∈c, ∃y∈d t=h(z)$\text{(hog)of (x)=(hog)[f(x)]=hog (y) =h[g(y)]=h(z)=t$
$\text{ho(gof) (x)=ho[g(f(x))]=ho[g (y)]=h[g(y)]=h(z)=t$
Donc, ∀x∈a\forall x \in a∀x∈a
$\text{(hog)of (x)=ho(gof) (x)$
Conclusion : $\text{(hog)of =ho(gof)$
La loi o est associative.
-
AAugustin1340 dernière édition par
Bonjour,
Merci pour toutes explications je vais ajouter tout ça à mes notes.
si maintenant je prends mon autre exercice, Si les 3 ensembles A,B,C sont en réalité un seul et même ensemble, est-ce que fo(gof)=(fog)of
Sa nous donnera ceci alors ?
-
mtschoon dernière édition par

La propriété d'associativité de la loi o est générale que les ensembles A, B,C soient distincts ou non (il n'y a pas d'exception).
Dans le cas particulier indiqué, Si A, B,C sont le même ensemble, ne parle pas de B et C dans les deux premières lignes .
De plus, si tu utilises seulement x et y, ne parle pas de z.Remarque
 j'ignore ce qui est demandé dan ton exercice, mais en principe, comme tout théorème, on utilise la propriété d'associativité de la loi 0 sans démonstration.*
j'ignore ce qui est demandé dan ton exercice, mais en principe, comme tout théorème, on utilise la propriété d'associativité de la loi 0 sans démonstration.*
-
AAugustin1340 dernière édition par
Je comprends vraiment pas ce que le prof demande...
Si les trois ensembles A,B,C sont en réalité un seul et même ensemble; est-ce que fo(gof)=(fog)oftoujours, parfois, jamais...
Quand le prof parle de 3 ensembles A,BC et puis qu'il dit que c'est en réalité un seul et même ensemble. Donc c'est A par exemple ?
-
mtschoon dernière édition par

Citation
Si les trois ensembles A,B,C sont en réalité un seul et même ensemble; est-ce que fo(gof)=(fog)ofLa réponse est OUI (toujours)
Effectivement tu peux dire que ces 3 ensembles sont A
-
AAugustin1340 dernière édition par
Ah, merci Mtschoon....

-
mtschoon dernière édition par

Bonjour,
Si ça t'arrange, je te mets une rédaction qui me semble correcte pour justifier directement le cas particulier dont tu parles
Vu que f et g sot deux applications de A dans A :
$\text{\forall x\in a \exists y\in a y=f(x)$
$\text{\forall y\in a \exists z\in a z=g(y)$
$\text{\forall z\in a \exists t\in a t=f(z)$1ere partie
$\text{(fog)of (x)=(fog)[f(x)]=fog(y)=f[g(y)]=f(z)=t$
2eme partie
$\text{fo(gof) (x)=f[gof (x)]=f[g(f(x)]=f[g(y)]=f(z)=t$
Conclusion:
$\text{\forall x\in a \exists t\in a (fog)of (x)=fo(gof) (x)=t$
D'où la conclusion souhaitée
-
AAugustin1340 dernière édition par
Bonsoir,
Oui ça m'arrange beaucoup, merci infiniment je vais noter tout ça dans mes notes et comprendre tout ça.

-
mtschoon dernière édition par

Bon travail !