topologie

Bonsoir,
je bloque sur cet exo:
Soit(xn), une suite d'un espace métrique (E,d).Cette suite converge vers a∈E si et seulement si
∀ε>0, ∃n∈N tel que ∀n≥N , d(xn,a)<ε
a)Donner la representation de la boule de centre O et de rayon r pour d∞
b) Donner la representation de la boule de centre O et de rayon r pour d1
c)Donner la representation de la boule de centre O et de rayon r pour d2

Merci d'avance!

Bonjour,

Pour la boule ouverte B(O,r), il s'agit de l'ensemble des éléments z de E vérifiant :
d(O,z) < r

Pour boule fermée B(O,r), il s'agit de l'ensemble des éléments z de E vérifiant :
d(O,z) ≤ r

Pour répondre à tes 3 questions, il faudrait savoir comment sont définies les distances d1 , d2, et d∞ , mais tu ne l'indiques pas...

j'ai écrit mon énoncé tel quel, il n'y a pas d'indication sur cela...

Si ces notations ne sont pas indiquées dans l'énoncé, je pense que c'est parce qu'elles ont été données dans ton cours (comme exemples usuels de distances).
Essaie de consulter ton cours.

Dans le cours on a donné la norme infinie, la norme 1, la norme i de maniere générale

Donne les définitions des normes (dont tu parles) pour pouvoir en déduire les distances associées.

|| x|| $∞_∞$ = Max{|x1|....|x2|}

|| x|| $_2$ = (∑ $x$ _i$$^2$)^{1/2}$ ,i allant de 1 à n

||x|| $_i$ = ∑| $x_i$ | , i allant de 1 à n

OK

a et b étant deux éléments de E :d(a,b)=||a-b||
z étant un élément de E, d(0,z)=||z||

Pour obtenir des boules ouvertes, tu dois donc expliciter**||z|| < r**
(sinon , tu mets ≤ au lieu de < pour des boules fermées)

Vu que l'on te demande des représentations dans un plan, on travaille dans R²

Soit z un élément (x,y) de R²

$d1(0,z)<r↔∣x∣+∣y∣<rd_1(0,z) \lt r \leftrightarrow |x|+|y| \lt r$

$d2(0,z)<r↔x2+y2<rd_2(0,z) \lt r \leftrightarrow \sqrt{x^2+y^2} \lt r$

$d∞(0,z)<r↔max∣x,∣y∣<rd_\infty(0,z) \lt r \leftrightarrow max{|x,|y|} \lt r$

Sauf erreur, tu dois obtenir le schéma donné.

Pour chaque boule,
Les points "extrêmes" situés sur l'axe des abscisses ont pour abscisses -r et +r
Les points "extrêmes" situés sur l'axe des ordonnées ont pour ordonnées -r et +r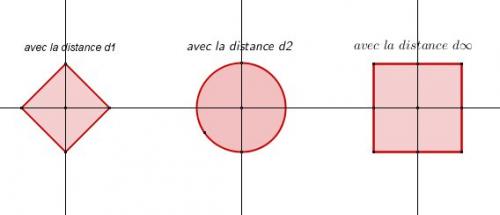

$fichier math$

Bon travail.

donc ici a quoi nous sert ceci:
"Cette suite converge vers a∈E si et seulement si
∀ε>0, ∃n∈N tel que ∀n≥N , d(xn,a)<ε"

et aussi si j'avais un centre qui n'est pas 0 que deviendront les distances

La définition de suite convergente n'a rien à voir avec les constructions des boules demandées.

Peut-être y a-t-il des questions prévues qui nécessitent cette définition ?

Si le centre n'est pas O, tu utilises la définition générale de distance :

a et b étant deux éléments de E : d(a,b)=||a-b||, en remplaçant a par le nouveau centre.

ok merci!

De rien !