Ensembles-Intersection
-
AAugustin1340 dernière édition par
Bonjour,
L'exercice est le suivant:
Peut-on conclure que A=B si A,B,C sont des ensembles comme:
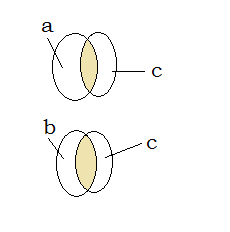
A∩C = B∩CJe me suis fais un dessin pour m'aider, donc oui A = B
A est dans l'intersection de C, donc A
B est dans l'intersection de C, donc B
Conclusion: A = B
-
mtschoon dernière édition par

Bonsoir,
La réponse est NON
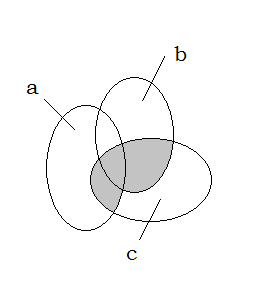
Pour t'en convaincre, représente les deux intersections demandées dans le schéma que je te joins.
(Remarque : le diagramme que tu as fait ne prouve rien car tu sembles avoir fait 2 schémas distincts alors que les ensembles A,B,C doivent être dans un même diagramme)
-
AAugustin1340 dernière édition par
Bonjour,
Merci, j'ai représenté les intersections dans le schéma donc effectivement c'est pas égal.
Maintenant comment je pourrais justifié avec une phrase ?
Je peux dire que A n'est pas égal à B vue que A ∩ C est une intersection de 2 ensemble A et C ,
B ∩ C est aussi une intersection de 2 ensemble B et C,
donc A ne peut être égal à B... :rolling_eyes:
-
mtschoon dernière édition par

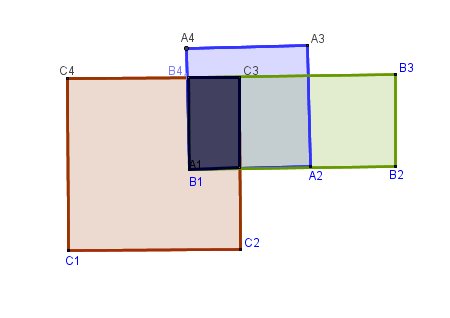
Je viens de te mettre unnouveau schéma dans mon message précédent.
Il n'est guère "beau" mais il me semble plus clair.L'ensemble C est l'intérieur du carré rose
CCC_1CCC_2CCC_3C4C_4C4L'ensemble B est l'intérieur du rectangle vert
BBB_1BBB_2BBB_3B4B_4B4L'ensemble A est l'intérieur du carré bleu
BBB_1AAA_2AAA_3A4A_4A4Ainsi, l'hypothèse A∩C = B∩C est bien réalisée (c'est l'intérieur du rectangle noir)
A n'est pas égal à B
-
AAugustin1340 dernière édition par
Merci pour tes schémas Mtschoon, et concrètement comment peut-on expliquer ça sans le schéma ? A part dire qu'il y a une intersections entre les 3 ensemble et que par conséquent A ne peut être égal à B, je vois pas trop ce que je peux ajouter d'autres ?
-
mtschoon dernière édition par

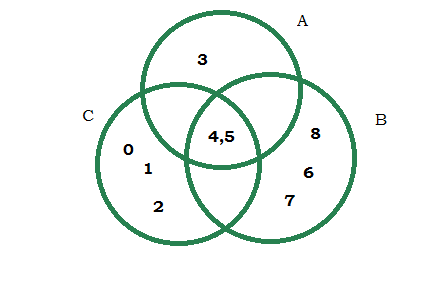
Sans le schéma , tu peux prendre un exemple numérique.
A={3,4,5}
B={4,5,6,7,8}
C={0,1,2,4,5}
A et B ne sont pas égaux (car pas les mêmes éléments)
Tu détermines A∩C et B∩C et tu constateras que A∩C=B∩C
-
AAugustin1340 dernière édition par
Bonsoir Mtschoon,
J'ai pris ton exemple numérique et j'y ai inclus un schéma pour m'exercer...
Que penses-tu ? Je pense que c'est exacte ?
-
mtschoon dernière édition par

C'est bon.
-
AAugustin1340 dernière édition par
Merci Mtschoon, je vais essayé de faire la même chose maintenant avec un Union pour m'exercer.
-
mtschoon dernière édition par

D'accord.