Etude de fonctions rationnelles

Bonjour,
Je suis bloqué sur cet exercice dont je ne comprends rien ca serait sympa si quelqu'un pouvait m'aider en me donnant des détails parce que je suis un peu mauvais merci d'avance à celui ou celle qui pourra m'aider.
Première partie.
On considère la fonction définie sur par : f (x) = 2x-3 le tout sur x² +10

Étudier les variations de f et dresser son tableau de variations.
Tracer la représentation graphique (Cf) de f dans un repère orthogonal. (unités : 1 cm sur l’axe
des abscisses et 10 cm sur l’axe des ordonnées).
Deuxième partie.
On considère maintenant la fonction g définie par : g (x) = 200 + 10 f (x).
Celle-ci représente le nombre de naissances par an dans un pays, avec g (x) en milliers de nouveau-nés et x = 0 en 2000.
Déduire le tableau de variations de g à partir de celui de f.
Indiquer les différentes phases de l’évolution des naissances dans ce pays entre 1990 et 2010.
x2 10
À long terme, le nombre de naissances dans ce pays a-t-il un plancher prévisible ? Si oui, lequel ?

Bonjour,

Tu dois bien savoir étudier une fonction :

f est définie sur R (car dénominateur non nul)

tu calcules la dérivée, tu détermines son signe et tu en déduis le tableau de variation.

Merci d'indiquer tes premiers résultats.

Pas de résultats à proposer ?

Si c'est le cas, je te suggère de commencer par revoir ton cours...

Comme je ne pourrai pas me connecter au forum pendant plusieurs jours, je te donne desindications pour faire cet exercice

$f(x)=2x−3x2+10f(x)=\frac{2x-3}{x^2+10}$

Pour tout x réel, le dénominateur est strictement positif donc ne s'annule pas.
La fonction f est donc définie sur R : Df=R

Pour calculer la dérivée, regarde ton cours sur**"dérivée d'un quotient"**

Tu dois trouver :

$f′(x)=−2x2+6x+20(x2+10)2f'(x)=\frac{-2x^2+6x+20}{(x^2+10)^2}$

Le dénominateur est strictement positif, donc le signe de f'(x) est le signe de son numérateur -2x²+6x+20

Tu regardes et appliques ton cours sur**"signe d'un polynôme du second degré"**

Connaissant le signe le f'(x), tu déduis automatiquement le sens de variation de f
(Pour les limites en -∞ et +∞, j'ignore si tu connais... à toi de voir)

Je te joins le tableau de variation de f que tu dois obtenir

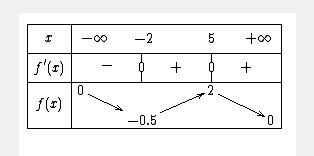
$fichier math$

(Faute de frappe : pour x=5,f(5)=0.2 au lieu de 2)

Je te joins une représentation graphique de f

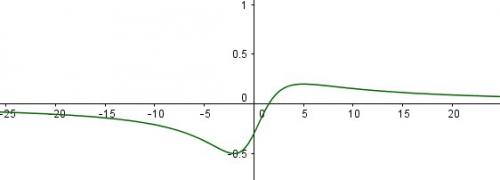
$fichier math$

La partie 2 de cet exercice est l'application de cette partie 1.

Comme je te l'ai déjà dit, revois ton cours d'abord, car sans maîtriser le cours on ne peut pas faire utilement des applications.

Bon courage !