Probabilités PACES

[Lucie]

Bonjour,
J'aurais besoin d'aide pour une question à laquelle je suis bloquée depuis quelques jours. Voici l'énoncé :

Un enfant a ingéré accidentellement l’un ou l’autre exclusivement de 3 médicaments A, B, C. Il avait à sa portée 4 boîtes de A, 2 boîtes de B et 4 boîtes de C.
Quelle est la probabilité qu’il ait ingéré le médicament A?
4/6
0,4
4
2/10
0,2
2
Les propositions A, B, C, D, E et F sont toutes fausses.

9. Les 3 médicaments entraînent des troubles digestifs dans 80% des cas avec A, dans 90% des cas avec B et jamais avec C. L’enfant ne présentant pas de troubles digestifs, quelle est la probabilité qu’il ait ingéré le médicament A?
   4/10
   64/100
   16/100
   8/100
   0,32
   8/10
   Les propositions A, B, C, D, E et F sont toutes fausses.

Donc pour la J'ai mis 0,4. Néanmoins, je n'arrive pas à résoudre la 9 sachant que la bonne réponse est 16/100.

Merci pour votre aide!!!

[mtschoon]

Bonjour,

8. Oui

9. Piste,

Tu dois calculer une probabilité conditionnelle

Pour clarifier le problème, je te conseille un arbre avec les données de l'énoncé

J'ai appelé T l'évènement "avoir des troubles digestifs"
J'ai appelé N l'évènement "ne pas avoir des troubles digestifs"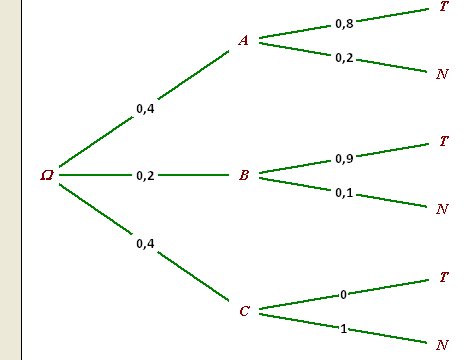

$\text{p(n)=(0.4\times 0.2)+(0.2\times 0.1)+(0.4\times 1)=...$

Ce que tu cherches est $\text{p_n(a)$ (probabilité de A sachant N)

$\text{p_n(a)=\frac{p(a\cap n)}{p(n)}$

Termine le calcul ( et tu trouveras bien la réponse que tu proposes)