3D Produit scalaire dans un cube

Bonsoir,

j'ai un problème avec un exercice corrigé en classe, où je ne comprends pas comment ont été trouvé des valeurs.

Calculer l'angle formé par 2 diagonales d'un cube de côté a.

il est noté en début de réponse :
AB $−a)\begin{pmatrix}a \ a \ -a \end{pmatrix}$
CD $a)\begin{pmatrix}-a \ a \ a \end{pmatrix}$

pour le reste je comprends les valeurs

merci

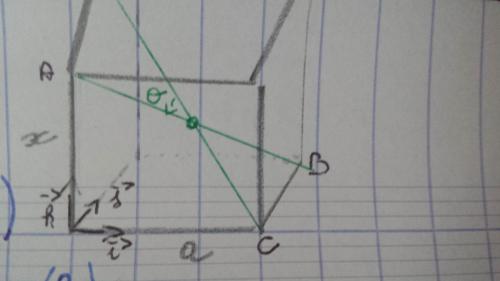
$fichier math$

Pour aider à la compréhension

Bonjour,

Ton graphique n'est pas complet.

Je suppose que la seconde diagonale est (CD) mais D ne figure pas dans ton graphique ...

Les coordonnées de A, B, C, D se trouvent parlecture graphiqueen fonction du repère choisi.

Tu dois lire

A(0,0,a)
B(a,a,0)
C(a,0,0)
D(0,a,a)

Conséquence ;

$ab⃗\vec{ab}$ a pour coordonnées (a-0,a-0,0-a)=(a,a,-a)

$cd⃗\vec{cd}$ a pour coordonnées (0-a,a-0,a-0)=(-a,a,a)

En exprimant le produit scalaire $ab⃗.cd⃗\vec{ab}.\vec{cd}$ de deux façons différentes, tu peux trouver l'angle θ

Première façon (avec les coordonnées)

$\text{\vec{ab}.\vec{cd}=a(-a)+a(a)+a(-a)=-a^2+a^2-a^2=a^2$

Deuxième façon (avec les normes et l'angle)

Tu dois savoir que les diagonales d'un cube de côté a ont pour mesure a√3

$\text{\vec{ab}.\vec{cd}=ab \times cd \times \cos \theta=a\sqrt 3 \times a\sqrt 3 \times \cos \theta=3a^2 \cos \theta$

DONC (en égalisant ces deux expressions)

$\text{a^2 \cos \theta =a^2$

$\text{\cos \theta =\frac{a^2}{3a^2}$

Après simplification par a²

$\fbox{\cos \theta=\frac{1}{3}}$

θ est l'angle dont le cosinus vaut 1/3

A la calculette, en degrés, et en utilisant la touche $cos^{-1}$ ou arccos (suivant les calculettes), tu trouves

θ≈70°5288

Remarque : cet exemple est très bien choisi car il montre l'intérêt du produit scalaire.

Bonjour Mtschoon,
Merci beaucoup, je me trompais dans le calcul de AB et CD , le reste je l'avais compris, mais vous le faite d'une autre méthode que mon enseignante, méthode qui est plus clair car à étapes.

C'est très bien si tout est clair pour toi.

Bon travail.