Géométrie Eclipse de Lune

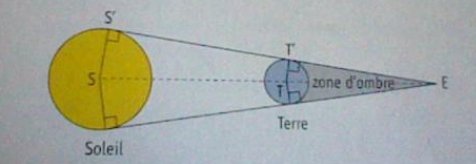
$fichier math$

Tiré du livre "Maths 4ème" des éditions Bréal, exercice n°107 de la page 177.

Coucou, ça fait des heures que j’essaye, mais je n'arrive pas à résoudre ce problème ^^'
Voilà l'énoncé du problème :

Le rayon du soleil [SS'] mesure 696 000 km, le rayon de la terre [TT'] mesure 6 360 km et la distance de la Terre au Soleil (ici TS) est de 149 600 000 km.

Je dois calculer la Longueur TE. Je pense qu'il faut que j'utilise un théorème, mais je ne suis pas vraiment sûre.

Ensuite,

Le centre L de la Lune est à environ 382 000 km de la Terre et le rayon de la Lune est environ de
1 738 km. Supposons que L appartient au segment [TE]. La droite parallèle à la droite (TT') et passant par L coupe la droite (T'E) en L'.
Calculer la longueur LL'. Par contre, je n'ai vraiment rien compris à cette partie là.

Il faut en déduire que, dans cette configuration, la lune se trouve entièrement dans la zone d'ombre. Il s'agit d'une éclipse totale de lune !

Voilà voilà, je vous remercie d'avance pour votre aide

scan modifié car ici, on ne doit scanner que les schémas.

Bonjour,

Dans cet exercice, tu dois utiliserl'application du théorème de Thalès aux triangles

Quelques pistes,

$\text{\frac{et}{es}=\frac{tt'}{ss'}$

OR $\text{es=et+ts$

donc

$\text{\frac{et}{et+ts}=\frac{tt'}{ss'}$

Tu remplaces TS, TT', SS' par leurs valeurs
Tu fais les produits en croix

Sauf erreur, tu dois trouver pour ET environ 1379641 km

Tu obtiens une équation qui te permettra de trouver la valeur de ET

Pour la lune, tu dois compléter le schéma

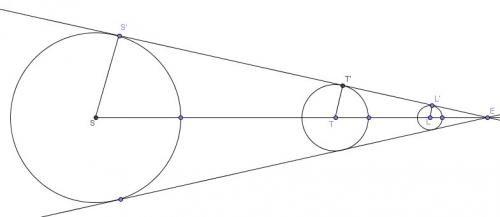
$fichier math$

Bon courage pour ces calculs un peu astronomiques...

J'ai fait le produit en croix pour ET, et j'ai trouvé 1 367 034 km...
Est-ce que c'est ça ?
Et pour l'équation, parlez-vous de ça :

$\text{\frac{et}{et+ts}=\frac{tt%27}{ss%27}$

Ou c'est quelque chose d'autre ?

Si la réponse que tu proposes est la valeur de TE , j'ignore tes calculs et la précision de ta calculatrice, mais ta proposition est raisonnable.
Comme déjà indiqué, ma calculette me donne 1 379 641 km .

Je reste perplexe sur la fin de ton message...

L'équation que tu indiques est l'équation pour calculer TE

Si tu parles d'une équation pour calculer LL' ce n'est évidemment pas celle là vu que LL' n'y figure pas.

Il faut utiliser encore le théorème de Thalès appliqué aux triangles, mais il faut utiliser les "bons" triangles.

Ah d'accord, merci beaucoup !
Je parlais de l'équation pour calculer TE, donc maintenant j'ai compris !

De rien !