Statistiques COUPURES médiane, quartile, quantile dans une liste de lettres

[Augustin1340]

Bonjour,

Je rencontre des problèmes lorsqu'il faut trouver la médiane, le quartile et le quantile.

Je voudrais d'abord bien comprendre la médiane. Je sais que la médiane est lequantile d'ordre 1/2

J'aimerais bien trouver la médiane pour ces 3 listes

a a b b | c c c d ici la médiane est b/c j'ai fait 0.5 * 8 = 4

a a b b b c c d ici la réponse est b/c je ne comprends pas ? Pour moi c'est b/b

a a b b b b c d ici la réponse est a/b & c/dje ne comprends pas comment on arrive à ce résultat ?

Merci d'avance

[mtschoon]

Bonjour,

Je te réponds mais ma réponse ne va pas te servir, je le crains...

Je t’indiquel’idée générale relative à la médiane, mais elle ne correspond peut-être pas à ton cours, car entre Belgique et France, il y a parfois des divergences de langage mathématique…

Pour déterminer une médiane M d'un ensemble de valeurs, il suffit d'ordonner les valeurs en une liste croissante (valeurs non groupées) et de choisir la valeur qui est au centre de cette liste, c’est à dire qu’il y ait autant de valeurs inférieures ou égales à M que de valeurs supérieures ou égales à M .

Pour une liste ordonnée de 2p+1 éléments (nombre impair d'éléments), la valeur du $(p+1{)}^{i\grave{e}me}$ élément est la médiane.

*Exemple :

Soit la liste 7 8 8 8 11 12 13 14
La médiane M est 11*

Pour une liste ordonnée de 2p éléments (nombre pair d'éléments), toute valeur comprise entre le p ${}^{i\grave{e}me}$ élément et ( $p+1{)}^{i\grave{e}me}$ élément est une médiane, d’après la définition donnée.
En pratique, dans le cas d'une liste de nombres, c'est la moyenne arithmétique de ces deux valeurs centrales qui est le plus souvent utilisée.

*Exemple :

Soit la liste 5 7 8 8 9 11 13 14 14 16
Toute valeur comprise entre 9 et 11 joue le rôle de médiane.
En prenant la moyenne entre ces deux valeurs: $\frac{9+11}{2}=10$,
la médiane M usuelle est 10*

Pour revenir à ton énoncé, il faudrait que tu donnes la définition exacte de ton cours relative à la médiane.

Je ne comprends absolument pas les notations utilisées...

Que veut direb/c , b/b, a/b & c/d ? ? ?

Sans connaître cela, je ne peux pas t'être utile...

[Augustin1340]

Bonjour Mtschoon,

Merci pour tes explications.

Voici l'énoncé de mon exercice:

Déterminer la coupure médiane. Cette coupure est-elle parfaitement médiane, ou bien quasi-médiane ?
Quelle est la proportion des obervations qui sont "à gauche" de la coupure ? Et "à droite" ?

Déterminer la première coupure quartile. Précisez si elle convient parfaitement ou si elle est "quassi". Quelle est la proportion
des observations qui sont "à gauche" de la coupure ? Et "à droite" ?

Déterminer la coupure quantile d'ordre 75 %. Cette coupure convient-elle parfaitement ou elle est quasi-quantile d'ordre 75 % ?
Quelle est la proportion des observations qui sont à "gauche" de la coupure ? et "à droite" ?

S'il s'agit d'une liste de socres et que le score "a" le meilleur et "e" le pire: que devez-vous faire pour me donner 20% qui ont
le mieux réussi ? Attention, vous ne pouvez pas faire de jaloux !

Admettons que j'aimerais bien déterminer la coupure médiane pour cette liste-ci.

a a b b b c c d

la réponse est visiblement b|c
Cependant, je ne comprends pas pourquoi c'est b | c ??
Pour moi la coupure est b|b ...

[mtschoon]

Merci pour l’énoncé qui est clair : il s’agit donc de coupures.

Il ne faut pas confondre médiane et coupure médiane.

Dans ma première réponse, je t’ai donné une définition usuelle de la médiane d’une série statistique.
Dans les exemples que tu proposes, il n’y a pas de médiane !
En effet, l’effectif étant de 8 (nombre pair), la médiane M doit se trouver entre la 4ème lettre et la 5ème lettre.
Or, dans ces exemples, M devrait être une lettre comprise entre b et c ou entre b et b .
C’est impossible, donc pas de médiane M.

Pour les coupures, je t’ai fait untableau pour chaque cas proposé dans ton énoncé.

1. Je t’explique le principe, avec le premier cas proposé (a a b b c c c d

TABLEAU

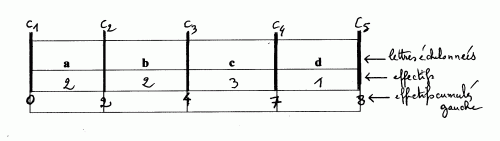
première ligne : les lettres échelonnées

deuxième ligne : les effectifs (un effectif par lettre)

troisième ligne : les effectifs cumulés gauche ( que l’on appelle aussi effectifs cumulés croissants)

Ils sont écrits sur les traits correspondants aux coupures (c1,c2,c3,c4,c5)
Explication :
effectif à gauche de c1 : 0
effectif à gauche de c2 : 2
effectif à gauche de c3 : 2+2=4
effectif à gauche de c4 : 2+2+3=7
effectif à gauche de c5 : 2+2+3+1=8 (effectif total)

La coupure médiane, lorsqu’elle existe est la coupure correspondant à l’effectif cumulé gauche égal au demi-effectif
L’effectif est n=8 donc n/2=4
Donc, la coupure médiane est c3 , que tu écris****b/c

2. Dansle deuxième cas proposé (a a b b b c c d)- effectif n=8 donc n/2=4

Il n’y apas de coupure médiane.
Dans ce cas, on chercheune
coupure quasi-médiane, ayant l’effectif cumulé gauche le plus proche de n/2, c’est à dire de 4 .
donc c3 est la coupure quasi-médiane que tu écris b/c

3. Dansle troisième cas (a a b b b b c d)- effectif n=8 donc n/2=4

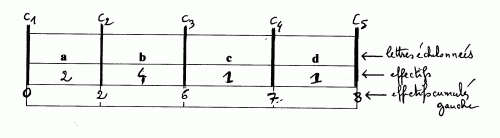
Il n’y a pas de coupure médiane.
Dans ce cas, on cherche à nouveau une coupure quasi-médiane, ayant l’effectif cumulé gauche le plus proche de n/2, c’est à dire de 4 .
On trouve deux coupures quasi-médianes , qui sont c2 et c3 , que tu écris a/b & b/c
Dans ta réponse proposée, tu as indiqué a/b & c/d … ? bizarre….bizarre...

Remarque ;: J’ignore la méthode de ton cours.
Il aurait été possible de faire aussi les effectifs cumulés droite , les fréquences cumulés gauche et les fréquences cumulées droite.

J’ai fait le plus simple possible, mais ce n'est pas facile d'expliquer un cours sur un forum !

Regarde tout cela de près et tiens nous au courant.

[Augustin1340]

Bonjour Mtschoon,

Un grand grand merci pour le temps que tu as consacré à me répondre.
Tu expliques vraiment très très bien. Mon prof est assez brouillon donc, je me permets de prendre des notes par rapport à tes explications.

Pour la question 3, effectivement c'est biena/b & b/cet non a/b & c/d.

Encore une fois merci beaucoup ^^

[mtschoon]

Contente que mes explications t'aient éclairé.

Maintenant que tu as compris les coupures médiane et quasi-médiane, je pense que tu n’auras pas de difficultés à comprendre les coupures quartiles et quantiles.

Si besoin, je t’indique ici les définitions relatives aux coupures quartiles.

Tu peux utiliser les 3 tableaux déjà faits pour tes 3 exemples. Tu n’as rien à faire d’autres. Tu tires seulement les conclusions.

Trois types de coupures quartiles.

I)Première coupure quartiledite aussi coupure quantile d’ordre 1/4 à gauche

C’est la coupure qui correspond à l’effectif cumulé gauche de n/4 (n étant l’éffectif total ).
Lorsqu’il n’y a pas de coupure première quartile, on cherche la (ou les) coupure quasi première quartile correspondant à l’effectif cumulé gauche le plus proche de n/4

II)Deuxième coupure quartiledite aussi coupure quantile d’ordre 1/2 à gauche
C’est la coupure médiane (cas déjà étudié).

III) Troisième coupure quartiledite aussi coupure quantile d’ordre 3/4 à gauche

C’est la coupure qui correspond à l’effectif cumulé gauche de 3n/4 (n étant l’effectif total ).
Lorsqu’il n’y a pas de coupure troisième quartile, on cherche la (ou les) coupure quasi troisième quartile correspondant à l’effectif cumulé gauche le plus proche de 3n/4

Entraîne toi à appliquer ces définitions sur les 3 exemples proposés.

*Je te rappellerai la définition générale de la coupure quantile avec un exemple, ultérieurement.
*
Bonne lecture.

[Augustin1340]

Merci Mtschoon depuis que j'utilise le tableau que tu m'as expliqué plus haut je comprends mieux, je suis capable de faire les exercices.

J'ai une vingtaine d'exercices (+ corrections) à faire, je vais m'entrainer de ce pas.

ps: Je n'ai pas besoin d'explications en plus pour cette fois-ci.

A bientôt

[mtschoon]

Daccord. Tu m'évites de t'indiquer le cas général des quantiles

En bref, j'ai l'impression que c'était la méthode des tableaux qui te manquait.

Bon courage Augustin pour tous tes exercices