domaine des Statistiques-Probabilités. Correction 1

Bonjour,

j'aimerais bien avoir une correction de mon exercice svp. Je vous remercie par avance pour le temps que vous consacrerez à le faire.

Exo1:

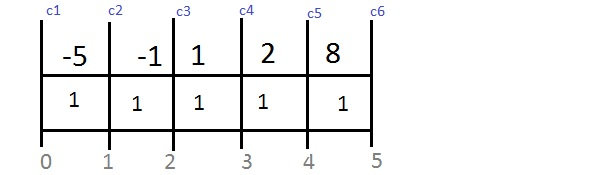
X(1) = -1 | X(2) = 2 | X(3) 1 | X(4) = 8 | X(5) = -5

Combien y a-t-il d’observation ? il y a 5 observations

Quelles sont les valeurs observables pour cette variable ?{-5,-4,-3,-2,-1,0,1,2,3,4,5,6,7,8 etc..}

**Quel est le type de cette variable ?**numérique discrète

Indiquez ci-dessous la liste de toutes les observations rangées ordinalement:

-5 -1 1 2 8

Quel est le mode ? Il s'agit de la valeur observée la plus fréquente . Ici je dirais 1 mais je ne suis pas sûr ? (1 et -1)

Moyenne ? (-5 + -1 + 1 + 2 + 8 ) = 5 5/5 = 1

Etendue ? 8 – (-5) = 13

Eam ? écarts des modalité à la moyenne (6 + 2 + 0 + 1 + 7) qu’on divise par le nombre d’observation 16/5 = 3.2 eam

Ecart type ? (1) je calcul d’abord la variance en prenant les carrés de toutes les observations et je divise ensuite par le nombre d’observation.
25 + 1 + 1 + 4 + 64 = 95/5 = 19
(2) ensuite je soustrais le carré des observations – la moyenne des observation (19 – 1) = 18 la variance fait 18
3) pour trouver l’écart-type on prend la racine carré de la variance donc 4,243

A partir d’ici je rencontre des petites difficultés…

Valeur médiane ? 1 car c'est l'observation centrale dans le rangement ordinal des 5 observations

La valeur que vous trouvez est-elle médiane ou quasi-médiane ? elle est médiane car il y a le même nombre d’observation à gauche et à droite

Coupure médiane ? c’est la coupure ½ ??? Voici le tableau

Bonjour,

Je regarde tes questions, mais toutes ne me semblent pas très pertinentes car les valeurs observées sont toutes différentes.

En plus, sans avoir le contexte, ce n'est pas possible de répondre à tout.

En cherchant sur le web, j'ai trouvé un exemple correspond assez bien à tes questions et plus intéressant car les valeurs observées ne sont pas toutes différentes.

Je te le joins.

http://jey.be/downloadseicw/market2/market2-doc-queststat1.pdf

Je regarde tes réponses (relatives à ton énoncé)

Oui pour le nombre d'observations.

Ne confonds pas les valeursobservablesavec les valeurs observées.

Il y a ici 5 valeurs observables qui sont ici 1,2,3,4,5

La variable est numérique mais pour dire si elle est discrète, sans le contexte, on ne le sait pas..
Tout dépend de ce que signifie X (et tu ne le donnes pas).

Imagine que les observations soient des relevées de températures en degrés [dans 5 lieux numérotés (1,2,3,4,5)], X serait continue

Imagine que les observations soient les niveaux (du sous-sous le plus bas jusqu'au dernier étage) de 5 appartements ou parkings, numérotés (1,2,3,4,5) d'un immeuble , X serait discrète.

Oui pour la liste

Vu que toutes les valeurs observées ont pour effectif 1, il n'y a pas véritablement de mode

Oui pour moyenne, étendue, Eam, Ecart-type et médiane.

Il n'y a pas de coupure médiane

Effectif total est n=5 donc n/2=2.5

Les deux valeurs correspondants aux effectifs cumulés gauche les plus proches de 2.5 sont c3 et c4 (c'est à dire -1|1 et 1|2) qui sont des coupures "quasi-médianes.

Bon travail !

Bonsoir Mtschoon,

Je me suis basé sur le site que tu m'as partagé. Cependant je souhaiterais utiliser des nombres négatifs. Car ceux-ci me posent souvent des problèmes.

Je vais m'inspirer sur l'une de tes propositions voici l'énoncer.

L’entreprise Nescologic souhaiterait relever le degré de température durant le début de l’hiver dans ses bâtiments.

Voici les observations :

X(1) = -1 | X(2) = 2 | X(3) 1 | X(4) = 8 | X(5) = -5

a) Quels sont les éléments observés ? Les 5 bâtiments de la Société Nescologic

b) Combien y a-t-il d’observation ? Il y a 5 observations

c) Quelle est la variable ? Le degré de température

d) Quelles sont les valeurs observables pour cette variable ? Les valeurs observables sont {1,2,3,4,5}

e) Quel est le type de cette variable ? numérique continues

f) Indiquez ci-dessous la liste de toutes les observations rangées ordinalement -5 -1 1 2 8

g) Mode ? il n'y a pas véritablement de mode, car toutes les valeurs observées ont pour effectif 1

h) Moyenne ? (-5 + -1 + 1 + 2 + 8 ) = 5 5/5 = 1

i) Etendue ? 8 – (-5) = 13

j) Eam ? écarts des modalité à la moyenne (6 + 2 + 0 + 1 + 7) qu’on divise par le nombre d’observation 16/5 = 3.2 eam

k) Ecart type ? (1) je calcul d’abord la variance en prenant les carrés de toutes les observations et je divise ensuite par le nombre d’observation.
25 + 1 + 1 + 4 + 64 = 95/5 = 19
(2) ensuite je soustrais le carré des observations – la moyenne des observation (19 – 1) = 18 la variance fait 18
3) pour trouver l’écart-type on prend la racine carré de la variance donc 4,243

l) Coupure médiane ? il n'y a pas de coupure médiane, il y a deux coupure quasi-médiane -1/1 et 1/2

m) Valeur médiane ? 1 car c'est l'observation centrale dans le rangement ordinal des 5 observations

n) Valeur que vous trouvez est-elle médiane ou quasi ? elle est médiane, car on retrouve le même nombre d'observation à gauche comme à sa droite.

Est-ce que tout ceci te sembles correcte ?

Merci d'avance

Tout cela me semble correct.

Bon dimanche !

Bonjour Mtschoon,

J'ai encore deux petites questions à corriger s'il te plait.

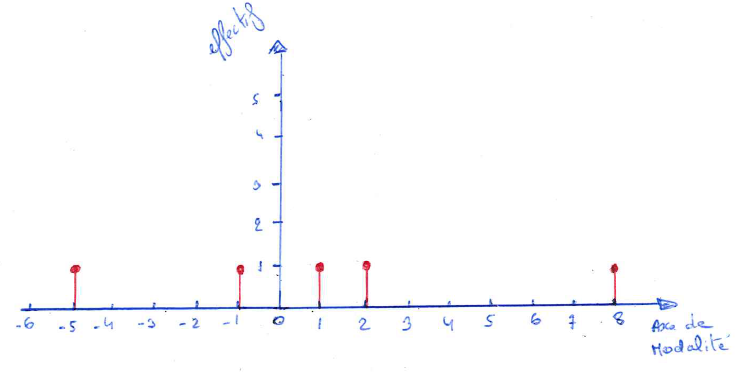
o) Représenter le diagramme en bâtonnets

p) Une erreur a eu lieu à l'encodage. Dans chaque bâtiment, on a relevé 8 fois plus de degrés. Qu'est-ce que cela modifie aux caractéristiques synthétique ?

Bonne journée à toi aussi

Pas tout à fait compris, on pourrait dire que les caractéristiques sont multipliés par 8.

Pour ton diagramme, la hauteur des bâtonnets est bonne mais place ces bâtonnets aux bonnes abscisses c'est à dire -5, -1, 1, 2, 8

Pour les nouvelles caractéristiques (après multiplication par 8 des valeurs de la variable), tu as peut-être des propriétés dans ton cours qui t'évitent de refaire tous les calculs.

Je reprends les réponses précédentes

a)b)c)d)e) sont inchangées

Pour f) les nouvelles valeurs de la variable sont -40,-8,8,16,64

Pour lemode, même réponse que précédemment vu que les effectifs sont toujours égaux à 1.

Pour moyenne, étendue, Eam, écart-type : tu multiplies par 8 les réponses précédentes.

il n'y a pas de coupure médiane, il y a deux coupures quasi-médianes $c_3$ et $c_4$ qui sont maintenant -8|8 et 8|16

Merci mtschoon pour tes corrections. Effectivement mon diagramme n'était pas correcte j'ai été trop vite.

Bonjour Augustin.

J'espère que tout va bien maintenant pour cet exercice.

En ce qui concerne ta dernière image, de chez moi, le site n'est pas accessible...

Bonjour mtschoon,

J'ai modifié le lien est-ce que c'est correcte ?

mtschoon

Je reprends les réponses précédentes

a)b)c)d)e) sont inchangées

Pour f) les nouvelles valeurs de la variable sont -40,-8,8,16,64

Pour lemode, même réponse que précédemment vu que les effectifs sont toujours égaux à 1.

Pour moyenne, étendue, Eam, écart-type : tu multiplies par 8 les réponses précédentes.

Pour la moyenne et l'écart-type ceux-ci ne bougent pas ?

Re-bonjour Augustin.

Oui , maintenant ton dernier graphique est visible et il est bon.

Pour la moyenne et l'écart-type, comme déjà indiqué, ils "bougent".

Pour obtenir la moyenne et l'écart-type de -40,-8,8,16,64, au lieu de faire les nouveaux calculs les concernant, tu peut prendre les réponses obtenues avec -5, -1, 1, 2, 8 et les multiplier par 8

Merci Mtschoon j'ai compris.

m(x) = 8
eam= 25.60
variance = 1152
écart-type = 33.941

C'est bon !