Calcul intégral -linéarisation de polynômes trigonométriques

Bonjour,
je viens de rentrer en école d'ingénieur et l'école part du principe que nous avons déjà étudié les intégrales et les primitives, ce qui est le cas pour un grand nombre mais pas pour la totalité de la classe.

Le problème c'est qu'on a pas vraiment de cours ou le peut qu'on a est incompréhensible pour quelqu'un qui découvre ce sujet.

Ce que je pense avoir compris, c'est qu'il y a 3 façon de calculer les intégrales: IPP, changement de variables et la méthode usuelle (je crois) pour les intégrales simples.

Mais comment choisir la méthode la plus appropriée? c'est à nous de déterminer le plus simple?

J'ai passé plusieurs heures à chercher sur internet comment faire mais je ne comprends toujours rien.

par exemple je ne vois absolument pas comment calculer ça:

$∫0pi/2cos2tdt\int_{0}^{pi/2}{cos^2t dt}$

$∫0pi/2sin3tdt\int_{0}^{pi/2}{sin^3t dt}$

la consigne est juste: calculer les intégrales

Si quelqu'un pouvait m'expliquer la démarche ça serait super.

Bonne journée

Bonjour,

Pour les intégrales que tu proposes, je te conseille d'employer la méthode de linéarisation (d'un polynôme trigonométrique)

Je te mets un lien à consulter (mais tu as peut-être aussi un cours)

http://villemin.gerard.free.fr/aMaths/Trigonom/aaaBases/Linearis.htm#cos3

L'idée est de passer par l'intermédiaire des complexes (formules d'Euler et formule du binôme) pour linéariser et ensuite trouver une primitive avec les formules usuelles.

Pour cos²x cette méthode générale n'est pas indispensable vu qu'il y a une formule usuelle qui fait le travail

$cos2t=1+cos(2t)2=12+12cos(2t)cos^2t=\frac{1+cos(2t)}{2}=\frac{1}{2}+\frac{1}{2}cos(2t)$

$\bigint_0^{\frac{\pi}{2}} cos^2tdt=[\frac{1}{2}t+\frac{1}{2}(\frac{1}{2}sin(2t))]_0^{\frac{\pi}{2}}=....=\frac{\pi}{4}$

Pour $sin^3$ t

Formule d'Euler :

$sint=eit−e−it2isint=\frac{e^{it}-e^{-it}}{2i}$

$sin3t=(eit−e−it2i)3sin^3t=(\frac{e^{it}-e^{-it}}{2i})^3$

Tu développes avec la formule du bonôme, tu simplifies le numérateur et tu regroupes les termes du dénominateur judisieusement.

Tu dois trouver :

$sin3t=(e3it−e−3it)−3(eit−e−it)−8isin^3t=\frac{(e^{3it}-e^{-3it})-3(e^{it}-e^{-it})}{-8i}$

Tu utilises à nouveau une formule d'Euler et tu dois obtenir:

$sin3t=−14sin(3t)+34sintsin^3t=-\frac{1}{4}sin(3t)+\frac{3}{4}sint$

Tu n'as plus qu'à chercher une primitive

Sauf erreur, tu dois trouver :

$j=\bigint _0^{\frac{\pi}{2}}sin^3t=....=\frac{2}{3}$

Bons calculs !

Bonjour Mtschoon,
et merci pour ces explications très détaillées. Néanmoins je n'ai pas compris grand chose car je n'ai pas fait grand chose en maths et je découvre tout ça comme la formule du binome, Euler etc...

pour reprendre le premier calcul vous dites:

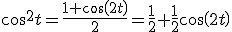
$fichier math$

mais je ne vois pas comment vous savez que cette formule (que je dois apprendre) =
$2cos(2t)\frac{\ 1}{\ 2} + \frac{\ 1}{\ 2}cos(2t)$

après dans votre intégrale vous mettez 1/2 t + 1/2 (1/2 .......)
Mais pourquoi mettre 3x 1/2 et pourquoi il y a 1 t sur la première fct.

Je suis navré c'est sûrement évident mais comme je vous le disais c'est vraiment nouveau pour moi.

Je pense qu'il faut que tu revois ton programme de maths de 1S/TS.
Tu ne peux pas faire d'exercices sans connaître les bases du cours.

Formule de duplication (conséquence de la formule d'addition cos(a+b)) :
cos(2t)=2cos²t-1 d'où cos²t=...

Une primitive de 1/2 est (1/2)t

Une primitive de cos(2t) est (1/2)sin(2t)

Je n'ai pas fait S, c'est bien pour ça que je suis perdu. c'est vraiment du nouveau. je vais essayer de me dépatouiller avec vos explications merci

Je suis désolé mais ça fait plus d'1 h que je cherche sur internet et je suis encore plus perdu que tout à l'heure.

comment sait-on que $\frac{e^i^\alpha + e^-i^\alpha }{2}$
= $eiαe^{i\alpha }$ =1

et que = $e−iαe^{-i\alpha }$ =cos 2 t

Il y a des confusions dans ce que tu as écrit...!

Notations exponentielles :

$\fbox{\cos \alpha +i\sin \alpha =e^{i\alpha}}$

$cos⁡(−α)+isin⁡(−α)=e−iα\cos(- \alpha) +i\sin (-\alpha) =e^{-i\alpha}$

Vu que $cos⁡(−α)=cos⁡α\cos(- \alpha)=\cos \alpha$ et que $sin⁡(−α)=−sin⁡α\sin (-\alpha)=-\sin \alpha$

la seconde égalité te permet d'écrire :

$\fbox{\cos \alpha -i\sin \alpha =e^{-i\alpha}}$

En retranchant membre à membre les 2 égalités encadrées et en divisant pas 2i, tu obtiens :

$\fbox{\sin \alpha=\frac{e^{i\alpha}-e^{-i\alpha}}{2i}}$

Si tu veux l'expression de cos α , il faut ajouter membre à membre les deux égalités encadrées au début de ce message et diviser par 2.

D'accord je commence à comprendre.

Mais je ne vois pas comment avec le résultat précédent 1/2 + 1/2 cos(2t)

Puis j'ai compris les primitives c'est à dire comment Cos 2t = 1/2 sin(2t)

Mais ce que je ne comprends pas c'est pourquoi on a 1/2 avant la primitive de Cos:
1/2(1/2sin(2t))

Merci

N'écris pas
Citation
Cos 2t = 1/2 sin(2t)

Ecris : une primitive de cos(2t) est 1/2 sin(2t)

Revois (ou vois...) les propriété des primitives.

Une primitive de 1/2 x cos(2t) est 1/2 x Primitive de cos(2t)

Je viens de comprendre le calcul ce qui donne en développant le résultat:

$\left[\frac{1}{2}t+ \right\frac{1}{/2 sin(2t)}]$

= 1/2 * pi/2 + 1/2 sin $p i$
= 1/2 * pi/2
pi/4

Par contre vous mettez 2 , 1/2:

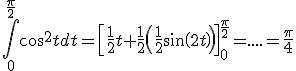
$fichier math$

J'ai bien compris que la primitive de 1/2cos(2t) est 1/2 * sin(2t) mais ça ne justifie pas le 1/2 avant la parenthèse. En tout cas j'ai l'impression d'avoir compris je suis content.

Je t'ai écris précédemment :

Citation
Une primitive de 1/2 x cos(2t) est 1/2 x Primitive de cos(2t)
Citation
une primitive de cos(2t) est 1/2 sin(2t)

Alors, réfléchis...

J'espère que ta réflexion t'a amené à la conclusion :

Une primitive de 1/2 x cos(2t) est 1/2 x Primitive de cos(2t) , c'est à dire 1/2 x 1/2 sin(2t)

Bonjour,
Je viens de prendre connaissance de vos messages.
Je pense que j'ai tous les éléments pour faire les autres calculs du même style.

J'ouvrirai d'autres sujets sur deux autres parties du TD : IPP et calculs d'integrales si je n'arrive pas à comprendre.

Merci pour votre aide et le temps passé.

Bon dimanche

Re-bonjour,
je m'entraine à calculer le (sin^3)t

En faisant la formule du binome je trouve:
$e3it+e−3it−3−8\frac{e^{3it}+e^{-3it}-3}{-8}$

Puis avec Euler:
$3cos(3t)−3−8\frac{3cos(3t)-3 }{-8}$

Je ne dois pas bien raisonner car je ne trouve pas vos résultat
c'est à dire -1/4.....

Merci

Bonsoir

Ta réponse obtenue avec la formule du binôme est fausse.

Je te précise la formule à utiliser :

$a-b)^3=a^3-3a^2b+3ab^2-b^3$

Recompte.

Cette formule m'a perdu définitivement !

qu'est ce que: a et b ?

a et b sont deux nombres quelconques

Ici :

$a=e^{it} \ b=e^{-it}$

Merci j'ai compris.

Juste une dernière petite question pour:
$∫0π2sin(t)∗cos(t)dt\int_{0}^{\frac{\pi }{2}}{sin (t)*cos(t)dt}$

Je fais 1 IPP et j'obtiens:
[sin pi/2 * sin pi/2] - [sin 0 sin 0]
je trouve 11 -0*0 =1
Mais on m'a dit que je devais trouver 1/2 mais je ne vois pas comment.

C'était la première fois que je faisais 1 IPP j'espère que la fin du calcul est bon pour 1 première fois.

IPP ? Quelle idée !

Il s'agit d'une primitive usuelle

fonction de la forme $u (t) u^{'} (t)$ donc primitive $12[u(t)]2\frac{1}{2}[u(t)]^2$

Le résultat est en effet $12\frac{1}{2}$

Remarque : si tu as d'autres questions, merci d'ouvre une autre discussion car ce topic devient trop long.