Le théorème de Tchébychev

Bonsoir,

Je dois pouvoir expliquer ce qu'est le théorème de Tchébychev et expliquer pourquoi c'est vrai.

Je dois par ailleurs, être capable de m'en servir pour divers exemples:

lors d'un pari à propos de la moyenne d'une série
lors d'un pari à propos d'un nombre extrait au hasard d'une liste
être capable de situer un sujet dans un groupe
expliquer par après pourquoi la note Z est un concept important
expliquer aussi, en quoi l'écart-type est bien une mesure de dispersion des observations autour de la moyenne.

Dans un premier temps ce qui m'intéresse, est la partie théorique.

Pour la partie théorique , j'ai indiqué ceci :

Le théorème de Tchebychev précise que 3/4 des observations sont dans l'intervalle [ n(x) - 2σ ; n(x) + 2σ ] ou moins d'un 1/4 en dehors.

On prend la moyenne et à partir de celle-ci , on prend 2 écart-type à gauche et à droite et on retrouve 3/4 des observations.
Le dénominateur du rapport correspond au carré du nombre d'écart-type, le numérateur est égal au dénominateur -1.

Autre exemple:

Soit 8/9 des observations sont dans l'intervalle [ n(x) - 3σ ; n(x) + 3σ ] ou moins d'un 1/9 en dehors.

Ce théorème justifie toute une série de chose, on sait que l'écart-type est une caractéristique de dispersion , dès lors , plus il est
petit, plus les variables sont concentrées près de la moyenne.

La note (Z) est un concept important, car elle permet de situer l'individu par rapport aux autres. Sa formule est (X(i) - n(x) ) / σ

14/20 est-ce une bonne note pour un bilan ?

A priori oui, mais grâce à cette formule, on peut vérifier si elle est est bonne par rapport aux autres membres de la classe.

Ainsi, on pourrait envisager que l'élève a une note Z de +1 et donc on déduit que sa note est bonne, ou bien peut-être que l'élève a une note Z de -3 et par conséquent sa note ne sera pas aussi bonne par rapport à l'ensemble des élèves.

Lors d'une interrogation j'ai eu 4 / 10 je comprends pas ???

Bonsoir Augustin,

Je n'ai absolument pas regardé les applications.
Je me contente de regarder ton titre :
"expliquer ce qu'est le théorème de Tchebychev et expliquer pourquoi c'est vrai."

Une remarque : la notation n(x) que tu utilises pour la moyenne me semble bizarre. Vu que le mot "moyenne" commence par m, je l'appelerais plutôt m(x) ou plus classiquement $x‾\overline x$

Dans cette partie théorique, je pense que ce ne sont pas seulement des exemples qu'il faut donner, mais commencer par donner la formule générale, c'est à dire le Théorème (que j'appelerais "Inégalité de Tchebychev")

Adapte car j'ignore les notations que tu utilises

Inégalité de Tchebychev
Pour une série S d'observations de moyenne $x‾\overline x$ et de variance $σ2\sigma ^2$ , pour tout t > 0, la proportion d'observations qui appartiennent à intervalle $[x‾−tσ,x‾+tσ][\overline x -t\sigma,\overline x +t\sigma]$ est supérieure ou égale à $1−1t21-\frac{1} {t^2}$

En conséquence, la proportion d'observations extérieures à intervalle $[x‾−tσ,x‾+tσ][\overline x -t\sigma,\overline x +t\sigma]$ est inférieure à $1t2\frac{1} {t^2}$

(Tu peux bien sûr ensuite, si tu le souhaites, mais seulement ensuite, illustrer ce théorème avec des exemples.)

Cela répond à la question "expliquer ce qu'est le théorème de Tchebychev"

Pour répondre à "expliquer pourquoi c'est vrai" , je pense qu'une démonstration mathématique est à faire.
Elle est peut-être dans ton cours. Regarde.

Bonsoir Mtschoon,

Je te remercie encore une fois pour tes explications précieuses et le temps que tu as consacré afin de me répondre.

C'est vraiment bizarre que mon professeur n'utilise pas le même vocabulaire/notation que vous autres en général. Nous avons reçu deux feuilles relatifs à l'inégalité de Tchébychev (si tu veux y jeter un oeil je peux te les envoyer par mp) , nous n'avons pas d'exemple concret ni de démonstration mathématique.

Si tu as le temps, j'aurais bien voulu avoir un exemple pour illustrer ce théorème et une petite démonstration pour que je puisse mieux comprendre.

Merci.

Bonjour Augustin,

Entre Belgique et France, et suivant les études poursuivies, ce n'est pas la première fois que l'on constate des différence de langage mathématique...Il faut adapter...

Peut-être sans le savoir clairement, tu as utilisé deux fois, par tes exemples, le théorème de Tchebychev.

1er exemple :
Soit une série d'observations telle que :
moyenne = $x‾\overline x$ =10
écart-type= $σ\sigma$ =1 (c'est à dire Variance=1²=1)

Soit I l'intervalle [8,12]
Si tu cherches la proportion d'observations qui appartiennent à intervalle I , tu dois prendre t=2
Après calcul de $1−1t21-\frac{1}{t^2}$ , tu trouves que la proportion d'observations qui appartiennent à intervalle I est supérieure ou égale à 3/4

2ème exemple
Soit une série d'observations telle que :
moyenne = $x‾\overline x$ =10
écart-type = $σ\sigma$ =1 (c'est à dire Variance=1²=1)

Soit I l'intervalle : [7,13]
Si tu cherches la proportion d'observations qui appartiennent à intervalle I , tu dois prendre t=3
Après calcul de $1−1t21-\frac{1}{t^2}$ , tu trouves que la proportion d'observations qui appartiennent à intervalle I est supérieure ou égale à 8/9

Je te propose une 3ème exemple à faire si tu le souhaites.
Soit une série d'observations telle que :
moyenne = $x‾\overline x$ =70
écart-type = $σ\sigma$ =15 (c'est à dire Variance=15²=225)

Soit I l'intervalle [55,85]
Pour t'entraîner, tu cherches la proportion d'observations qui appartiennent à cet intervalle .

Tiens nous au courant de cela.
Ensuite, si tu veux, je te proposerai une démonstration "mathématique" du théorème, mais, si tu ne l'as pas vu en cours, on ne va pas te la demander un contrôle.
Vu ce que tu indiques, pour justifier le "pourquoi c'est vrai", je pense qu'une vérification sur un exemple sera suffisante.

Bon travail et bonne année 2018 !

Bonjour Mtschoon,

Joyeuse année également et merci encore pour ton aide.

Bonsoir Augustin,

Calcul des deux premiers exemples :

Pour le premier exemple:
t=2
Je te fais le calcul :
$1−1t2=1−122=1−14=44−14=341-\frac{1}{t^2}=1-\frac{1}{2^2}=1-\frac{1}{4}=\frac{4}{4}-\frac{1}{4}=\frac{3}{4}$
Tu tires la conclusion

Pour le second exemple:
t=3
Je te fais le calcul :
$1−1t2=1−132=1−19=99−19=891-\frac{1}{t^2}=1-\frac{1}{3^2}=1-\frac{1}{9}=\frac{9}{9}-\frac{1}{9}=\frac{8}{9}$
Tu tires la conclusion

Bonsoir Mtschoon,

Je pense avoir compris, l'exercice 3 voici mon raisonnement qu'en penses-tu ?
text alternatif

A propos du dernier exercice voici comment je procède:
moyenne = $x‾\overline x$ =70;
écart-type = $σ\sigma$ =15 ;
intervalle [55,85];

$x‾\overline x$ - t * $σ\sigma$ = 55
70 - t * 15 = 55
70 - 55 = 15
15 = 15 t
$1515=\frac{15}{15}=$ t
$1−1t2=01-\frac{1}{t^2}=0$

$x‾\overline x$ + t * $σ\sigma$ = 85
70 + t * 15 = 85
15t = 85 - 70
15t = 15
t = $1515\frac{15}{15}$
$1t2=1\frac{1}{t^2}=1$

Oui, tes réponses sont bonnes
t=1, $1−1t2=01-\frac{1}{t^2}=0$ et $1t2=1\frac{1}{t^2}=1$
Tu peux déduire que pour t=1, les informations données par le théorème ne sont guère pertinentes. C'est le cas "trivial".
(Le théorème donne un résultat pertinent pour t > 1)
(La proportion d'observations qui appartiennent à intervalle [55,85] est supérieure ou égale à 0.
La proportion d'observations extérieures à cet intervalle est inférieure à 1)

Tu aurais pu peut-être rédiger plus simplement et faire un schéma explicatif mais l'essentiel est que tu y arrives.

Je te fais un 4ème exemple (le dernier)
moyenne = $x‾\overline x$ =70;
écart-type = $σ\sigma$ =10
intervalle= [55,85]

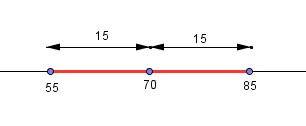
$tσ=15t\sigma=15$
$t=15σ=1510=1.5t=\frac{15}{\sigma}=\frac{15}{10}=1.5$

D'où :
$1t2=1−11.52=0.555...\frac{1}{t^2}=1-\frac{1}{1.5^2}=0.555...$
$1t2=11.52=0.444...\frac{1}{t^2}=\frac{1}{1.5^2}=0.444...$

Conclusions :
La proportion d'observations qui appartiennent à intervalle [55,85] est supérieure ou égale à 55% environ
La proportion d'observations extérieures à cet intervalle est inférieure à 44% environ

Je pense que tu as bien compris.

Merci de m'indiquer si tu souhaites consulter la démonstration mathématique du théorème ou bien une vérification du théorème avec un exemple concret, pour répondre à "expliquer pourquoi c'est vrai"

J'obtiens bien les mêmes réponses que toi.

1))

70 - t * 10 = 55
70 - 55 = 10t
$1510\frac{15}{10}$ = t
1 - $11,52\frac{1}{1,5^2}$ = 0.555

2))

70 + t * 10 = 85
15t = 85 - 70
t = $1510\frac{15 }{10}$
t = 1,5
$11,52\frac{1}{1,5^2}$ = 0.444

Je vais également utiliser ton schéma que tu m'as présenté lors de l'ancien exercice.
Pour moi cette partie-ci est comprise, je te remercie pour tes explications j'ai enfin compris comment ça fonctionnait.

ps: je vais ouvrir un nouveau topic pour avoir une idée de la démonstration du théorème pour prouver que c'est vrai.

Bonne soirée à toi et encore merci.

D'accord pour la vérification souhaitée et à bientôt.

Encore merci pour ton aide.

De rien et bon courage pour les calculs de la vérification .