Relation d'equivalence

Bonjour,
j'ai un problème sur un exercice d'annale:

Sur l'ensemble $X={0,1,2,3}$ on considère la relation R = {(0,2), (2,3), (3,2), (3,3)

a) Dessinez le graphe de la relation $R$

b) Quelle est la matrice de la relation $R$

c) Quelle est la plus petite relation d’équivalence sur $X$ contenant $R$ ? (la réponse peut être donnée sous forme ensembliste ou graphique ou matricielle, à votre choix).

d) On note $R^{'}$ la relation d'équivalence déterminée à la question $C$ . Trouvez un ensemble $Y$ et une fonction $f : X$ -> $Y$ tels que $x R^{'} y$
SSI $f (x) = f (y)$

Pour les questions a et B c'est bon.
Par contre pour les 2 dernières....

A ce que j'ai pu voir sur internet ce sont des maths générales.

Merci par avance.

Bonjour,

Piste pour c)

Pour c), tu complètes pour obtenir unre relation d'équivalence c'est à dire une relation réflexive, symétrique et transitive.

R = {(0,2), (2,3), (3,2), (3,3)}

Pour obtenir une relation reflexive, tu dois compléter avec (0,0), (1,1), (2,2)

Pour obtenir une relation transitive, tu dois compléter avec (0,3) (ainsi (0,2) et 2,3) -> (0.3)

Pour obtenir une relation symétrique, tu dois compléter avec (2,0), (3,0)

Vérifie que je n'ai rien oublié. et fais l'illustration que tu préfères.

Lorsque tu auras bien maitrisé la c), on passera à la d)

Je n'ai absolument aucune idée de comment faire des matrices avec ce nouveau site mais je trouve.

R': 1 0 1 1
0 1 0 0
1 0 1 1
1 0 1 1

C'est donc grâce à cette nouvelle matrice qu'on peut déterminer la plus petite relation d’équivalence? comment?

Pour écrire les matrices, le nouveau site n'a pas encore prévu.
ça viendra, j'espère...

Peut-être devrais-tu revoir les définitions relatives aux relations d'équivalence.

La plus petite relation d’équivalence est déjà trouvée...elle correspond aux 10 couples obtenus : Le minimum de couples a été ajouté pour satisfaire la définition de relation d'équivalence
Au final
0 R' 0
0 R' 2
0 R' 3
1 R' 1
2 R' 0
2 R' 2
2 R' 3
3 R' 0
3 R' 2
3 R' 3

Revois tout ça de près.

Voila le schéma qui m'a permis de trouver la matrice
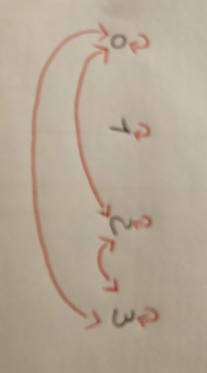
0_1515519453924_Capture du 2018-01-09 18-36-43.png

De plus je ne vois pas le 0 R' 1
Par contre je trouve bien les 10 couples avec ce schéma.

Ton schéma est bon
Effectivement, 0 R' 1 n'existe pas
Pour la matrice , il y a bien dix "1" et le reste en "0" , mais j'ignore la disposition utilisée.
Si tu as mis 0 1 2 3 (en haut en horizontal (valeurs de départ) et
0
1
2
3 (en vertical (valeurs d'arrivée),
ta matrice est bonne.

J'ai bien positionné la matrice comme vous l'indiquer.
Super cette question est comprise
pour la d)
Donc il faut faire un ensemble pour trouver 10 couples? avec quelles valeurs?

Pour le d), tu cherches une fonction ( pour toi synonyme d'application, d'après ton précédent topic) de X vers Y.
X={0,1,2,3}
C'est donc l'image de chacune des quatre valeurs 0,1,2,3 qu'il faut trouver.

Piste, liée à R'
A la valeur 0, tu peux faire correspondre l'ensemble des éléments qui lui sont associés : f(0)={0,1,2,3}
A la valeur 1, tu peux faire correspondre l'ensemble des éléments qui lui sont associés : f(1)={1}
etc

Essaie de poursuivre dans cette voie.

,

Donc si j'ai compris pour la question d) la réponse attendue est:
f(0)= {0,2,3}
f(1)={1}
f(2)={0,2,3}
f(3)={0,2,3}

est ce bien ça?

Tout à fait.

Tu peux déduire un ensemble Y qui convient et t'assurer que la condition x R' y <=> f(x)=f(y) est bien satisfaite.

aucun ensemble de X est égal à Y

Ta phrase est vraiment confuse...

Pour Y, tu peux prendre: Y = { {0,2,3} , {1} }

{0,2,3} correspond au f(0)
Mais pourquoi {1} ???
si c'était Y={{0,2,3},{2}} je comprendrais peut-être mais là je ne sais pas

f(0)= {0,2,3}
f(1)={1}
f(2)={0,2,3}
f(3)={0,2,3}

L'image de 0 par f est {0,2,3}
L'image de 1 par f est {1}
L'image de 2 par f est {0,2,3}
L'image de 3 par f est {0,2,3}

Pose-toi la question : quel est l'ensemble des images ?

donc si f(2)= {4} et f(3)= {5}
On aurait noté Y={{0,2,3},{1},{4},{5}}
Si on ne prend que f(0) et f(1) c'est que f(0)=f(2)=f(3)
Est ce bien ça?

Je pense que tu as compris

Si f(0)={0,2,3} , f(1)={1} , f(2)={4} ,f(3)={5}, effectivement on peut prendre Y={{0,2,3},{1},{4},{5}}

(On peut bien sûr aussi prendre pour Y un ensemble de parties de X contenant {0,2,3},{1},{4},{5} et d'autres parties en plus)

Merci beaucoup Mtschoon.
Bon week-end

De rien ! Bon week-end à toi.