Relation de préordre

Bonsoir à tous,
je suis en train de réviser pour le DS de la semaine prochaine. Jusqu'à qu'un de mes camarades me pose une question sur cet exercice.

Sur l'ensemble X={a,b,c,d,e,f} on définit la relation binaire R={(a,b),(a,c),(c,d),(e,d),(f,g)}

Quelle est la relation de préordre engendrée par R?
Quelle est la relation d'équivalence engendrée par R?

Concernant la 2) vous me l'aviez expliqué il y a très peu de temps. Il faut la compléter pour obtenir 1 relation réflexive, transitive et symétrique.

Donc il suffisait juste que je me rappelle du terme préordre pour la 2 ème question.

La déf du cours est: Soit R 1 relation binaire, quelconque sur X, la relation de préordre engendrée par R est la + petite relation reflexive , transitive qui contient R on la note R*

Cela signifie qu'il faut faire comme pour la 1er sans faire la symètrie?

Merci

Bonjour Dut,

Effectivement, une relation de pré-ordre doit être réflexive et transitive (si elle était, en plus anti-symétrique, ce serait une relation d'ordre)
Une relation d'équivalence doit être réflexive, symétrique et transitive.

Dans les deux cas, il faut compléter.

Tu travailles comme c'est indiqué dans l'énoncé.

Commence par le pre-ordre (question 1)
Ensuite, pour la question 2), tu complèteras les couples trouvés à la 1) avec des couples qui rendront cette relation symétrique.

Bonjour,
voila ce que je trouve: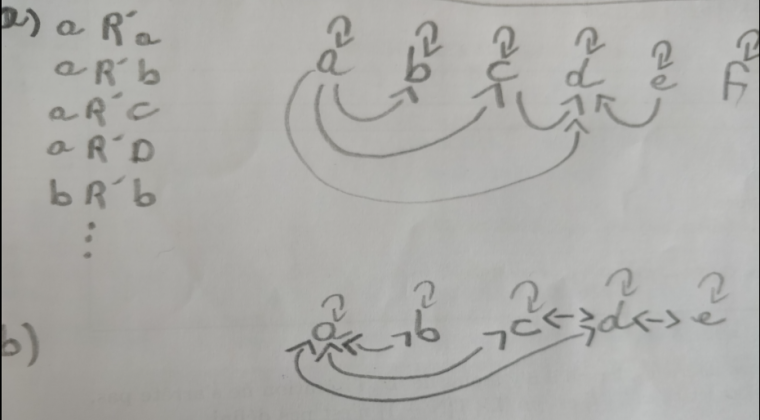

Par contre le (f,g) de la consigne me pertube vu qu'il n'y a pas de g on ignore (f,g)?

@dut

Pour f R g, c'est visiblement une erreur de l'énoncé.

X aurait dû s'écrire : {a,b,c,d,e,f,g} (ou alors, il ne fallait pas écrire (f,g).

Le plus simple est de ne pas tenir compte de g.

Je regarde la première question : réflexive st transitive

Oui pour réflexive car tu as bien complété avec aRa,bRb,
cRc,dRd,eRe,fRf

Pour la transitivité, il il manque des couples.Vérifie !

Il manque bRc puis bRd puis aRe puis cRe

Pour la seconde question, tu dois recopier tout le schéma fléché de la première question et compléter avec les flèches pour obtenir en plus la symétrie.
(aRb est complété avec bRa, aRc avec cRa, etc,etc).
Je crois que c'est ce que tu as fait, mais comme la première question n'est pas complète, la seconde ne l'est pas non plus.

C'est compris encore une fois merci.

De rien et bon DS !