Fonctions PORTE et transformées de Fourier correspondantes
-
Rraphael3 dernière édition par mtschoon
Bonjour j'ai pu trouver plusieurs exemples sur internet mais je ne comprends pas toujours comment trouver toutes les valeurs.
Par exemple pour:
f(t)= PORTE (3t-5)La hauteur sera celle par défaut par la porte car in n'y a pas de coeff devant PORTE.
Pour le centre il faut faire 3/5, mais je ne sais pas comment trouver les deux bornes avant et après 3/5.Merci par avance pour votre aide
-
Rraphael3 dernière édition par
Après avoir pris le temps de poser le problème, j'ai trouvé comme solution:
7/6 le centre de la fct porte: 3/5 11/6
cela est-il juste?
-
mtschoon dernière édition par mtschoon

Bonjour Raphael,
Visiblement, tes sujets sont relatifs aux signaux, et les mathématiques appliquées aux signaux ne font pas partie de mon domaine...Sans le cours, ce n'est pas commode !
J' ai trouvé une définition de la fonction TABLE (notée en général Π\PiΠ, sur le web).
J'espère qu'elle correspond à ton cours. Vérifie.
Π(t)=1 pour−1/2≤t≤1/2\Pi(t)=1\ pour -1/2\le t\le 1/2Π(t)=1 pour−1/2≤t≤1/2
Π(t)=0 ailleurs\Pi(t)=0 \ ailleurs Π(t)=0 ailleursTu veux analyser la fonction définie par t ->Π(3t−5)\Pi (3t-5)Π(3t−5)
Calcul relatif à l'intervalle :
−1/2≤3t−5≤1/2-1/2 \le 3t-5 \le 1 /2−1/2≤3t−5≤1/2
En ajoutant 5 : 9/2≤3t≤11/29/2 \le 3t \le 11 /29/2≤3t≤11/2
En divisant par 3 : 3/2≤t≤11/63/2\le t \le 11 /63/2≤t≤11/6Bilan :
Π(3t−5)=1 pour 3/2≤t≤11/6\Pi(3t-5)=1\ pour \ 3/2\le t\le 11/6Π(3t−5)=1 pour 3/2≤t≤11/6
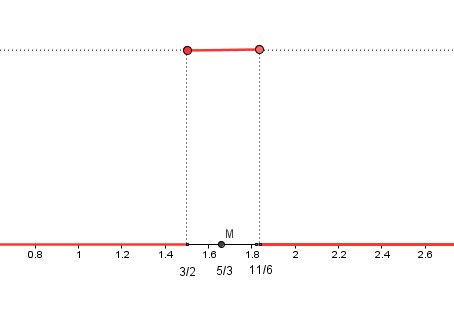
Π(3t−5)=0 ailleurs\Pi(3t-5)=0 \ ailleurs Π(3t−5)=0 ailleursReprésentation graphique (en rouge)
 url de l'image)
url de l'image)
Le "milieu" M a pour abscisse 3/2+11/62=5/3\frac{3/2+11/6}{2}=5/323/2+11/6=5/3
-
Rraphael3 dernière édition par raphael3
Bonjour Mstchoon et merci Pour cette explication c'est entierement ca.
Par contre je ne comprends pas comment on obtient les resultats en divisant par 3.
car je fais 9/2/3 n'est pas egal a 27/2 mais ce n'est pas ça qu'il faut faire mais je ne sais pas comment faire autrement.Car 9/3 font 3 ce qui justifierai le 3/2 mais le 11/6 je ne le comprends pas
-
mtschoon dernière édition par mtschoon

923=9231=92×13=3×3×12×3=32=1.5\LARGE\frac{\frac{9}{2}}{3}=\frac{\frac{9}{2}}{\frac{3}{1}}=\frac{9}{2}\times \frac{1}{3}=\frac{3\times 3 \times 1}{2 \times 3}=\frac{3}{2}=1.5329=1329=29×31=2×33×3×1=23=1.5
Si tu préfères
923=4.53=1.5\LARGE \frac{\frac{9}{2}}{3}=\frac{4.5}{3}=1.5329=34.5=1.5
-
mtschoon dernière édition par mtschoon

Pour 11/6...
C'est le même principe
1123=11231=112×13=11×12×3=116\LARGE\frac{\frac{11}{2}}{3}=\frac{\frac{11}{2}}{\frac{3}{1}}=\frac{11}{2}\times \frac{1}{3}=\frac{11\times 1}{2\times 3}=\frac{11}{6}3211=13211=211×31=2×311×1=611
-
Rraphael3 dernière édition par raphael3
j'ai compris et j'ai pu tracer le graphe identique au votre merci.
Il était demandé après le graphe de calculer la transformée de Fourier de cette fonction.
Un de mes camarades qui avait deja fait un peu de fourier m'a envoyé son cours de l'année derniere.
Il y a noté que pour la porte le domaine de Fourier associé est : sinc (PI f)
Et que le retard est e^(-2 pi j f to ) S(f)Je suppose qu'il faut utiliser ces 2 éléments mais je ne sais pas comment ?
Si vous pouvez encore m'aider ça serait très gentil!
-
mtschoon dernière édition par mtschoon

Ces transformations de Fourier sont certainement très utiles aux électroniciens, mais comme déjà dit, ce n'est pas mon domaine.
En regardant les définitions sur le web,on peut lire :
En appelant F cette transformée,
F(f)=∫−∞+∞s(t)e−j2πftdtF(f)=\displaystyle\int_{-\infty}^{+\infty}s(t)e^{-j2\pi ft}dtF(f)=∫−∞+∞s(t)e−j2πftdt
( f pour fréquence et s pour signal)Vu le signal étudié,
F(f)=∫3/211/61e−j2πftdt=∫3/211/6e−j2πftdtF(f)=\displaystyle\int_{3/2}^{11/6}1e^{-j2\pi ft}dt=\displaystyle\int_{3/2}^{11/6}e^{-j2\pi ft}dtF(f)=∫3/211/61e−j2πftdt=∫3/211/6e−j2πftdtEn faisant le calcul direct de primitive, on obtient
F(f)=−12πjf[e−2jπft]3/211/6F(f)=\frac{-1}{2\pi j f}[e^{-2j \pi f t}]_{3/2}^{11/6}F(f)=2πjf−1[e−2jπft]3/211/6
On termine le calcul numérique et éventuellement on transforme les termes de la forme e−jθe^{-j\theta}e−jθ en cosθ−isinθcos \theta-isin\thetacosθ−isinθ
Je t'indique cette "méthode mathématique" pour le principe, mais vu les indications que tu donnes , ce n'est pas la méthode à utiliser (tu n'est pas obligé de faire le calcul intégral direct).
Dans le cours, il doit y avoir une formule (toute faite) pour la transformée de Fourier de la fonction PORTE de base (celle qui vaut 1 entre -1/2 et +1/2 et 0 ailleurs.) : cela correspond à ta première indication
Ensuite, il doit y avoir des propriétés pour passer de la fonction TABLE de base à celle que tu étudies: cela correspond à ta seconde indicationN'ayant pas le cours, je ne peux que te laisser trouver...
Bon courage !
-
Rraphael3 dernière édition par
Merci,
Il a juste projeté quelques slides sur le tableau mais nous avons rien de concret. Le problème c'est que je n'ai jamais ça donc je ne comprends pas comparé aux autres.
Il ne faut pas utiliser sinc ? je suis un peu perdu mais si vous ne pouvait pas faire plus ce n'est pas grave vous m'avez quand meme aidé
-
mtschoon dernière édition par mtschoon

Le sinc dont tu parles intervient dans la transformation de Fourier de la fonction PORTE de base
En faisant le calcul intégral avec la fonction PORTE de base, j'ai trouvé sin(πf)πf\frac{sin(\pi f)}{\pi f}πfsin(πf) qui doit s'appeler sinc(πf)sinc (\pi f)sinc(πf)
(c'est la première indication)Il te reste à trouver comment tu dois passer de ce signal PORTE de base à celui que tu étudies.
II doit y avoir une propriété prévue dans ton cours.(qui sera la seconde indication)
-
Rraphael3 dernière édition par mtschoon
voila une partie du cours d'un de mes camarades de ses années antérieures:
(scan supprimé)Je n'ai pas l'impression que cela aide pour calculer la transformée de Fourier mais bon. Malheureusement je trouve ce document inabordable pour quelqu'un découvrant Fourier
-
mtschoon dernière édition par mtschoon

Effectivement, ce document ne sert pas ici : il concerne la dérivation .
Tu n'a rien à dériver dans ta question !
Tu devrais plutôt chercher des théorèmes relatifs aux changements d'échelle (on dit aussi dilatations) et aux translations (on dit aussi décalages) pour passer passer de la PORTE de base à la PORTE demandée.Remarque : je ne crois pas qu'il soir autorisé de scanner un cours sur le forum. Je le supprime.
-
Rraphael3 dernière édition par
http://perso.univ-lemans.fr/~berger/Signal_MP2/TFourier/co/TFUsuelle.html
ce site donne la TF de la porte simple, donc si je comprends bien c'est identique au site en prenant en compte le 3t-5 qui est le retard?
-
mtschoon dernière édition par mtschoon

Ce site confirme qu'il n'y a pas d'erreur dans la réponse donnée pour la fonction PORTE simple(de base): la transformée de Fourier est bien sinc(πf)sinc(\pi f)sinc(πf)
(la fréquence f s'appelle autrement dans le site, mais c'est pareil).
J'ignore les termes"techniques" à employer, mais il faut que tu trouves dans ton cours les théorèmes que je t'ai demandé précédemment.
Lorsque tu les auras trouvés, ton problème sera réglé.
-
Rraphael3 dernière édition par
Qu'est ce que je me sens idiot de patauger comme ça

Je vais essayer de chercher sur les quelques notes de cours que j'ai essayer de prendre.
-
Rraphael3 dernière édition par mtschoon
Désolé par avance si le scan n'est pas autorisé je vous laisserai le supprimer mais juste pour être sûr que je ne parte pas dans une mauvaise direction
(scan supprimé)
-
mtschoon dernière édition par mtschoon

Tu "patauges" parce que tu ne connais pas le cours et comme je ne l'ai pas, ça complique..
Effectivement, il faut que tu trouves les propriétés à utiliser.
Si besoin, regarde le lien ici :
http://www.geea.org/IMG/pdf/Cours_TS.pdf
A la page 10, paragraphe 2.2.2, tu as un tableau donnant les propriétés de la transformation de Fourier.
Tu cherches Dilatation et Translation.
Avec ça, tu dois pouvoir arriver à tes fins.Je te joins un schéma.
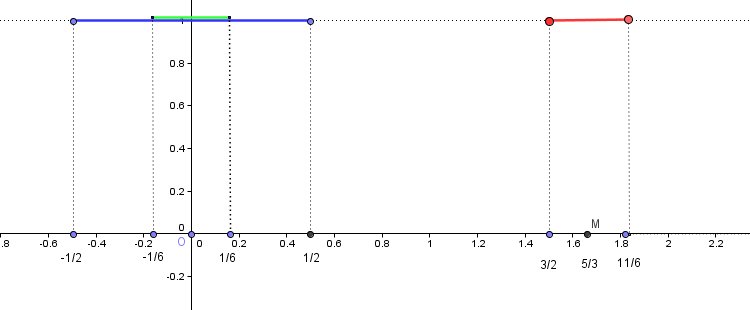
Le signal PORTE de base est en bleu (largeur 1 de la porte, "centre" 0)
Le signal PORTE "dilatée" est en vert (largeur 1/3 de la porte, "centre" O)
Le signal de la PORTE dilatée maintenant "Translatée" est en rouge (largeur 1/3 de la porte, "centre" M)Remarque :
Nos réponses se sont croisées..
Pour la "dilatation" (qui est appelé "changement d'échelle" ici) , la propriété scannée supprimée que tu as donnée est bonne.
-
Rraphael3 dernière édition par
en fait mon problème c'est que en regardant le scan sur le changement d'échelle je ne vois pas comment mettre en rapport avec la fonction de la porte que j'ai.
-
mtschoon dernière édition par mtschoon

Pour passer de la porte (bleue) de largeur 1 à la porte verte (de largeur 1/3) le changement d'échelle est simple.
En utilisant les notations du lien que je t'ai donné :
Pour passer de la porte bleu à la porte verte, tu utilises la "dilatation" avec a =3
La transformée est donc 13sinc(πf3)\frac{1}{3}sinc(\pi \frac{f}{3})31sinc(π3f)Pour passer de la porte verte à la porte rouge tu utilises la translation avec b=5/3
La transformée est donc e−2jπ53f×13sinc(πf3)e^{-2j\pi \frac{5}{3} f}\times \frac{1}{3}sinc(\pi \frac{f}{3})e−2jπ35f×31sinc(π3f)
-
Rraphael3 dernière édition par
Je vais essayer de comprendre maintenant.
Merci beaucoup pour votre aide précieuse
Bonne soirée
-
Rraphael3 dernière édition par raphael3
Bonsoir, j'ai compris je viens de trouver le même résultat par contre je ne sais pas le faire de manière calculatoire avec des integrales.
Merci beaucoup pour votre aide à bientot
-
mtschoon dernière édition par mtschoon

Tu n'es pas obligé de faire le travail avec le calcul intégral.
Les propriétés se démontrent avec le calcul intégral (conséquence de la définition qui est une intégrale), mais dans la mesure où elles font partie de ton cours, il te suffit de les utiliser "toutes faites", c'est le but (à condition de les connaître bien sûr !).Tu as bien travaillé !