Traitement du signal - Fourier/ signal rectangulaire

Bonjour j'ai un exercice dont je ne comprends pas l'énoncé ou plutôt l'équation donné.
Etant donné que c'est du traitement du signal en rapport avec du Fourier peut être que vous pourrez m'aider.

L'énoncé est:

Soit une transmission d’un signal binaire 01100010 en bande de base avec :
g([0, π/8[) = 0; g([π/8, 3 ∗ π/8[) = 1; g([3 ∗π/8, 6 ∗ π/8[) = 0; g([6 ∗ π/8, 7 ∗ π/8[) = 1; g([7 ∗ π/8, π[) = 0.

1.Représentez g(t)
2.Calculer le coefficient de Fourier A 0 .
3.Calculer les coefficients de Fourier A n .
4.Calculer les coefficients de Fourier B n .
5.Donner le diagramme spectral de l’amplitude des harmoniques d’ordre 0 à n = 10.

Pour la 1ere question qui n'est peut être pas la plus intéressante en passant je ne sais pas ce qu'est g(t), peut-être la somme de tous les g?

Merci par avance.

Bonjour Dut,

Tu ne sais pas ce qu'est g(t) ??? Cette fois, c'est indiqué!
L'énoncé t'indique :
Soit une transmission d’un signal binaire 01100010 en bande de base avec :
g([0, π/8[) = 0; g([π/8, 3 ∗ π/8[) = 1; g([3 ∗π/8, 6 ∗ π/8[) = 0; g([6 ∗ π/8, 7 ∗ π/8[) = 1; g([7 ∗ π/8, π[) = 0.

Cela veut dire que :
pour t compris entre 0 et $π\pi$ /8 , g(t)=0
pour t compris entre $π\pi$ /8 et $3π3\pi$ /8 , g(t)=1
pour t compris entre 3 $π\pi$ /8, et $6π6\pi$ /8 , g(t)=0
pour t compris entre 6 $π\pi$ /8 et $7π7\pi$ /8, g(t)=1
pour t compris entre 7 $π\pi$ /8 et $π\pi$ , g(t)=0

Tu n'as plus qu'à faire la représentation graphique
Il faudra faire attention que sur chaque "marche" horizontale, le point de gauche est pris et celui de droite n'est pas pris .

Merci Mtschoon j'ai compris. C'était juste une incompréhension d'écriture.
Par contre comment tracer g(t), il y a t-il un logiciel pour ça?

Il n'y a vraiment besoin de rien, vu sa simplicité.!

Si ça t'arrange, je te joins une représentation graphique (en rouge) sur [0, $π\pi$ [, c'est à dire sur une période.

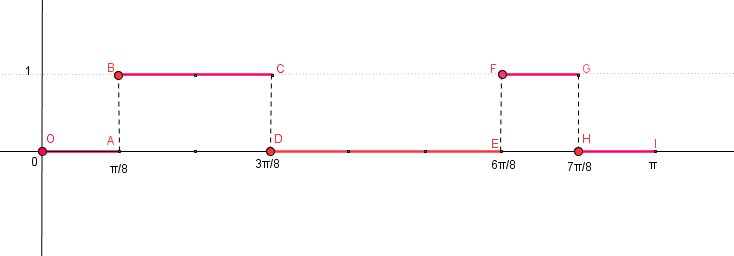
Assure toi de la comprendre.

Quel est le logiciel que vous avez utilisé? cela pourra sûrement me servir si je suis amené à tracé des signaux plus complexes.
Merci beaucoup pour vos explications.
Bonne soirée.

Pour faire un schéma correct (pour l'enregistrer sur le forum), je l'ai fait avec Geogebra, mais un papier, une règle et un crayon suffiraient pour la compréhension...

Bonne soirée.

Pour calculer les c****oefficients de Fourier, les formules sont écrites dans la discussion précédente.

Ici,
la période est $π\pi$ , donc tu remplaces T par $π\pi$
la fréquence f vaut $1T\frac{1}{T}$ donc tu remplaces f par $1π\frac{1}{\pi}$ , ce qui donne une simplification par $π\pi$ .
Tu intègres entre 0 et $π\pi$ (vu la période)

Tu peux donner tes calculs et/ou réponses si tu as besoin d'une vérification.

Merci beaucoup

De rien !

(Lorsque tu auras le temps, assure toi de bien savoir calculer les coefficients de Fourier et l'amplitude des harmoniques)

Bonjour, j'avais laissé cet exercice en suspens à cause des rattrapages.

Premièrement comment faite vous pour déterminer que la période est Pi?

Pour A0 = $∫π/83π/8g(t)dt\displaystyle\int_{\pi /8}^{3\pi /8}g(t) dt$
Si j'ai bien compris les bornes sont déterminées grâce à la valeur 1 de l'énoncé?

Que dois je faire après?

Merci

Bonjour,
Regarde l'énoncé.
On te donne la fonction sur [0 $π[\pi[$ (et sur cet intervalle où il n'y a pas de "répétition").
Il est "sous-entendu", que le phénomène se répète d'où
période= $π\pi$

Pour $A_0$ , la formule que tu donnes n'est pas bonne.
Relis ma réponse, sur cette discussion, qui date de 25 jours.

$T=πT=\pi$

La formule générale te permet d'écrire :

$A0=1π∫0πg(t)dtA_0=\frac{1}{\pi}\displaystyle \int_0^\pi g(t)dt$

Sur les intervalles où g est nulle, l'intégrale est nulle

Il reste
$]A_0=\frac{1}{\pi}[\ \displaystyle \int_{\pi/8}^{3\pi/8}1 dt+\displaystyle \int_{6\pi/8}^{7\pi/8}1 dt \ ]$

Tu peux faire le calcul des intégrales avec les primitives.
Ici, le plus simple est d'utiliser l'interprétation avec les aires

$]A_0=\frac{1}{\pi}[\ aire(ABCD)+aire(EFGH)\ ]$

Sauf erreur, après simplification, tu devrais trouver $A_0=3/8$

Bonsoir Mtschoon pour A0 j'ai un doute avec 3pi/8

Bonne soirée

Bonsoir Dut ,

Attention : il y a une simplification par $π\pi$

La réponse n'est pas 3 $π\pi$ /8 , mais 3/8

Revois tes calculs si besoin.
L'aire d'un rectangle est longeur x largeur.
Tu dois calculer l'aire des deux rectangleset multiplier par 1/ $π\pi$

$A0=1π[1×(3π/8−π/8)+1×(7π/8−6π/8)]A_0=\frac{1}{\pi}[1\times (3\pi/8-\pi/8)+1\times (7\pi/8-6\pi/8)]$

$A0=1π[2π/8+π/8]A_0=\frac{1}{\pi}[2\pi/8+\pi/8]$

$A0=1π[3π/8]A_0=\frac{1}{\pi}[3\pi/8]$

$A_0=3/8$

Bonjour,
Je vois d'où vient mon erreur, merci.

Si je ne me suis pas trompé pour la suite je trouve pour:
An= (racine(2)) / pi . n . f

et pour Bn = -(racine(2)) / pi . n . f

Je n'ai pas eu le temps de faire les calculs de An et Bn aujourd'hui (je le ferai dès que possible), mais je peux te dire tout de suite que tes réponses sont à revoir.

Merci c'est gentil. Mince, je tenterai de refaire les calculs demain

Je te calcule An

Vu la longueur, je ne peux pas tout détailler...je fais au mieux.

Par définition (formule dans le topic précédent)
$An=2T∫Ig(t)cos(2πnft)dtA_n=\frac{2}{T}\displaystyle\int_I g(t)cos(2\pi nft)dt$
I est un intervalle de longueur une période

Ici, la période T vaut $π\pi$
On peut prendre $I=[0,π]I=[0,\pi ]$
la fréquence $f$ vaut : $f=1T=1πf=\frac{1}{T}=\frac{1}{\pi}$

d'où $An=2π∫0πg(t)cos(2πn1πt)dtA_n=\frac{2}{\pi}\displaystyle\int _0^{\pi}g(t)cos(2\pi n\frac{1}{\pi}t)dt$

En simplifiant par $π\pi$

$An=2π∫0πg(t)cos(2nt)dt\boxed{A_n=\frac{2}{\pi}\displaystyle\int _0^{\pi}g(t)cos(2 nt)dt}$

Sur les intervalles où g(t)=0, forcémment le produit $g (t) c o s (2 n t)$ vaut 0, donc l'intégrale faut 0

Il reste à faire le calcul sur les deux intervalles où g(t)=1

$An=2π[∫π/83π/81cos(2nt)+∫6π/87π/81cos(2nt)dt]A_n=\frac{2}{\pi}[\displaystyle\int _{\pi/8}^{3\pi/8}1cos(2 nt)+\displaystyle\int _{6\pi/8}^{7\pi/8}1cos(2 nt)dt]$

$An=2π[∫π/83π/8cos(2nt)+∫6π/87π/8cos(2nt)dt]\boxed{A_n=\frac{2}{\pi}[\displaystyle\int _{\pi/8}^{3\pi/8}cos(2 nt)+\displaystyle\int _{6\pi/8}^{7\pi/8} cos(2 nt)dt]}$

Maintenant, il faut que tu te souviennes de la méthode pour calculer une intégrale en utilisant une primitive de la fonction à intégrer.

Rappel :
la variable étant t, a étant une constante non nulle, une primitive de $c o s (a t)$ est $1asin(at)\frac{1}{a}sin(at)$

$∫π/83π/8cos(2nt)[12nsin(2nt)]π/83π/8=12n[sin(2n3π/8)−sin(2nπ/8)\displaystyle \int_{\pi /8}^{3\pi /8}cos(2nt)[\frac{1}{2n}sin(2nt)]_{\pi /8}^{3\pi /8}=\frac{1}{2n}[sin(2n3 \pi /8)-sin(2n\pi /8)$

$∫π/83π/8cos(2nt)=12n[sin(3nπ/4)−sin(nπ/4)]\displaystyle \int_{\pi /8}^{3\pi /8}cos(2nt)=\frac{1}{2n}[sin(3n\pi /4)-sin(n\pi /4)]$

De la même façon, tu dois trouver
$∫6π/87π/8cos(2nt)=12n[sin(7nπ/4)−sin(6nπ/4)]\displaystyle \int_{6\pi /8}^{7\pi /8}cos(2nt)=\frac{1}{2n} [sin(7n\pi /4)-sin(6n\pi /4)]$

Tu remplaces dans An .
En mettant $12n\frac{1}{2n}$ en facteur puis en simplifiant par 2, sauf erreur, tu dois trouver :
$An=1πn[sin(3nπ/4)−sin(nπ/4)+sin(7nπ/4)−sin(6nπ/4)]\boxed{A_n=\frac{1}{\pi n}[ sin (3n\pi /4)-sin(n\pi /4)+sin(7n\pi /4)-sin (6n\pi /4)]}$

Revois tout cela de près.
Pour Bn, tu appliques la même méthode sachant qu'une primitive de $s i n (a t$ ) est $\frac{1}{a}cos(at)$

Bonjour Mtschoon,
Merci pour cette explication très détaillée. Je vais mettre ce long WE à profit pour essayer de refaire le calcul et le comprendre.
J'aimerais aussi tracer le diagramme spectral des harmoniques. Je sais qu'il faut que je remplace le n des formules de An et Bn par des entiers. Sur quel logiciel peut-on tracer ce style de diagramme?

Bonjour Dut,

Tu ne peux pas bruler les étapes.

Pour tracer le diagramme spectral des harmoniques (pour n allant de 1 à 10) , tu n'auras aucun problème si tu arrives à calculer , pour tout n, $An2+Bn2\sqrt{A_n^2+B_n^2}$ (c'est cela qui est difficile !)

Tu n'auras pas besoin de logiciel particulier, vu qu'il s'agit seulement de faire 10 traits verticaux (10 petits bâtons verticaux, si tu préfères).
En abscisse, tu placeras les valeurs 1,2,...,10 correspondant aux rangs des harmoniques.
En ordonnée, tu prendras les amplitudes des harmoniques c'est à dire $An2+Bn2\sqrt{A_n^2+B_n^2}$ pour n=1,2,...,10

Personnellement, comme déjà dit, pour faire une représentation graphique correcte pour enregistrer sur le forum je prends geogebra, mais sur papier, une règle et un crayon suffisent .

Tu ne pourras faire ce diagramme que lorsque tu auras fait tout ce qui précède, c'est à dire les calculs de $A_n$ $B_n$ , puis $An2+Bn2\sqrt{A_n^2+B_n^2}$

A la calculette par exemple, tu remplaceras n par 1,2,...,10 dans la formule de $An2+Bn2\sqrt{A_n^2+B_n^2}$ trouvée.

Alors, pour le WE, comme tu dis, essaie de comprendre $A_n$ et de faire $B_n$ Ce sera déjà une étape de franchie

Ensuite, il faudra passer à $An2+Bn2\sqrt{A_n^2+B_n^2}$ qui sera une nouvelle difficulté "trigonométrique"...

Enfin, il y aura le petit diagramme qui sera l'illustration graphique de tout cela.

Bon travail !

Merci beaucoup Mtschoon.
Je vais essayer de tout faire dans l'ordre.
Joyeuses Paques

Merci et Joyeuses Pâques à toi aussi