Maths discrètes - Dénombrements

[dut]

Bonsoir,
Les résultats du DS n'ont pas été assez haut je dois donc aller aux rattrapages.
Malgré votre aide sur cette partie 3) questions me posent problèmes car sauf erreur de ma part je n'ai jamais eu à les traiter dans ce style d’exercice.

Soit X={a,b,c}
6) combien y a t il de fonction vers {1,0}?
7) Combien y a t'il de relations binaires sur X?
Combien y a t il de relations d'équivalence sur X?

Peut être si vous avez 2 minutes vous pourrez aussi vérifier les résultats des questions précédentes:
2)mots de longueur 4 sur X contenant au plus 1 fois la lettre a? -> 189
3) combien de parties de X?-> 8
4) combien de parties de X de cardinal 4? Aucune
5) Combien de parties de X contenant au plus une fois l'élément a? -> 8, pour moi c'est la même question que la 3

Merci si vous avez le temps de jeter un coup d'oeil.

[mtschoon]

Bonjour,

"Jeter un coup d'oeil " ! ! !
Si je ne fais que jeter un coup d'oeil, je crains que tu ne comprennes pas grand-chose ....

Je regarde dans l'ordre numérique des questions posées.

Indique ta démarche pour la 2) ta réponse me semble très bizarre...

3)4)5) : c'est bon

6)7)8) : c'est plus délicat

Pour la 6)
je crois me souvenir que dans ton cours, "fonction" veut dire "application" c'est à dire que chaque élément de départ doit avoir une image.

Tu raisonnes

a a deux images possibles (0 ou 1)
lorsque l'image de a est choisie, b peut avoir 2 images possibles (0 ou 1)
lorsque les images de a et b sont choisies, peut avoir 2 images possibles (0 ou 1)
Bilan :$2\times 2\times 2=2^3=8$

(tu pourrais faire un arbre de choix pour cela, mais je ne sais pas si tu as l'habitude)

[mtschoon]

Pour la 7 )

Fais un tableau rectangulaire
Ligne horizontale où tu mets a b c
Ligne verticale où tu mets a b c

Tu obtiens ainsi 9 cases vides.

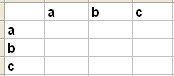
Tu peux penser mettre dans chaque case Oui ou Non suivant que la relation R est réalisée ou pas ( si tu préfères pense Vrai ou Faux, ou bien 1 ou 0)

Tu raisonnes

Dans la case (a,a) , on peut mettre Oui ou Non (2 possibiltés)
Lorsque la réponse de la case (a,a) est choisie, on peut mettre Oui ou Non dans la case (a,b) donc encore 2 possibiltés
etc , etc,

Bilan : $2\times 2\times 2\times 2\times 2\times 2\times 2\times 2\times 2=2^9=512$

[mtschoon]

Pour la 8 )

Il faut trouver, parmi les 512 relations binaires, celles qui sont réflexives, symétriques , transitives.

Utiliser encore le tableau avec les 9 cases vides de la question 7)

Pour la réflexivité, il faut qu'il y ait Oui dans les cases (a,a), (b,b), (c,c)
Les autres cases peuvent avoir Oui ou Non

Bilan : $1\times 2\times 2\times 1\times 2\times 1\times 2\times 2\times 2\times 1=2^6=64$

Parmi ces 64 relations, il faut trouver celles qui sont, en plus, symétriques.

Le tableau doit être symétrique par rapport à la diagonale principale
(la case (a,b) doit être identique à la case (b,a), la case (a,c) doit être identique à la case (c,a), etc, etc

On ne compte donc que la diagonale ( avec des Oui ) et un triangle de 3 cases (avec Oui ou Non par case)

Bilan : $1\times 2\times 2\times 1\times 2\times 1=2^3=8$

Parmi ces 8 relations, il faut trouver celles qui sont, en plus, transitives.
Là, il faut trier !

Lorsqu'il y a Oui dans la case (a,b) et Oui dans la case (b,c), il faut Oui dans la case (a,c)
Lorsqu'il y a Non dans las case (a,b), il peut y avoir Oui ou Non dans la case (b,c), et Oui ou Non dans la case (a,c)

Bilan $(1\times 1\times 1)+(1\times 2\times 2)=1+4=5$

La réponse à la question 8 ) est donc $5$

J'ai expliqué le mieux possible mais ce n'est pas simple sur un forum...j'espère que tu vas comprendre...

[dut]

Merci Mtschoon,
J'ai recompté le 2) je trouve 48:
je décompose le calcul en 2:
-1er cas il n'y a pas de a -> 2⁴
-2ème cas il y a 1 a: 4(possibilité de placement) *2³
Soit 48 en réponse finale.

Pour les 3 autres je pense avoir compris. J'ai eu du mal avec la 8 mais je pense que c'est bon de toute façon je n'ai pas le choix, je vais rabâcher pour être bien sur. En tout cas merci pour la qualité des explications

[mtschoon]

C'est bien 48 pour la 2 ) et ton explication est bonne.

Si tu veux t'entraîner (en plus) sur cette partie, je te donne des résultats:
le nombre total de mots de 4 lettres est $3^4=81$
le nombre de mots de 4 lettres contenant exactement deux a est $6\times 2^2=24$
le nombre de mots 4 lettres contenant exactement trois a est $4\times 2=8$
le nombre de mots 4 lettres contenant exactement quatre a est 1

Tu peux ainsi retrouver la réponse à la question posée
$81-(24+8+1)=81-33=48$

Reposte s'il y a quelque chose de pas clair et Bon Courage !

[dut]

Merci pour tout.

[mtschoon]

De rien !