Relation d'équivalence - image réciproque

Bonsoir,
Je fais le DS que j'ai eu en début d'année et dont un exercice m'a posé problème (principalement sur la formulation des questions).

Soit X l'ensemble de nombres X={1,2,3,4,5,10,100,1000} on définit la fonction f: X -> N par : f(x) = le nombre de lettres dans l'écriture de x en français.

a) remplir un tableau de 3 lignes comme suit:

1ère ligne: x élément de X
2ème ligne: l'écriture de x en français
-3ème ligne: La valeur de f(x)
x 1 2 3 4 5 10 100 1000
fr un deux trois quatre cinq dix cent mille
f(x) 2 4 5 6 4 3 4 5

b) Quelle est la partition de X fournie par les images réciproques de f?
j'ai regardé sur internet la définition de image réciproque mais ce n'est toujours pas clair.

c) Dans cette relation d'équivalence, quelle est la classe de 1000?
Je ne comprends pas le mots classe

Merci par avance

Bonjour,

Oui pour a)

b) Pour l'image réciproque, je te mets un lien à consulter qui me parait intéressant.
http://www.bibmath.net/dico/index.php?action=affiche&quoi=./i/image.html

Pour ta question,

La fonction est f
L'ensemble de départ est X=E={1,2,3,4,5,10,100,1000}
L'ensemble d'arrivée est F={2,3,4,5,6}

Chaque élément de E a une image, par f, dans F
je t'ai fait un schéma fléché de la situation .
J'ai disposé les éléments de E de façon que les flèches ne se mélangent pas.
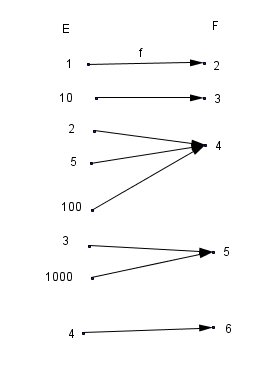
0_1520842239575_flèches.jpg

Pour l' image réciproque de f
Tu pars d'un élément de F et tu cherches ses antécédents dans E
antécédent de 2 : 1
antécédent de 3 : 10
antécédents de 4 : 2,5,100
antécédents de 5 : 3,1000
antécédent de 6 : 5

$f^{-1}$ est la notation pour la réciproque de f
Tu peux écrire, entre parties concernées :
$f−1({2})={1}f^{-1}(\lbrace 2\rbrace)=\lbrace1\rbrace$
$f−1({3})={10}f^{-1}(\lbrace 3\rbrace)=\lbrace10\rbrace$
$f−1({4})={2,5,100}f^{-1}(\lbrace 4\rbrace)=\lbrace2,5,100\rbrace$
$f−1({5})={3,1000}f^{-1}(\lbrace 5\rbrace)=\lbrace3,1000\rbrace$
$f−1({6})={4}f^{-1}(\lbrace 6\rbrace)=\lbrace4\rbrace$

L'ensemble de départ X (que j'ai noté E pour que cela soit les mêmes notations que dans le lien que je t'ai donné), a été ainsi "partagé" en 5 parties disjointes dont la réunion vaut X
$X=E={1}∪{10}∪{2,5,100}∪{3,1000}∪{4}X=E=\lbrace1\rbrace \cup \lbrace10\rbrace \cup \lbrace2,5,100\rbrace\cup\lbrace3,1000\rbrace\cup\lbrace4\rbrace$

On dit qu'on a fait ainsi une partition de X

c)Tu parles de relation d'équivalence mais tu ne la nommes pas...
Cette relation d'équivalence dans E pourrait s'appeler "avoir même image que" (et on peut justifier que c'est bien une relation réflexive, symétrique , transitive).
Les 5 parties de E indiquées dans la question b) s'appellent des classes d'équivalence
La classe de 1000 est donc la partie ${3,1000}\lbrace3,1000\rbrace$

J'ai compris merci beaucoup pour les explications.
Bonne soirée

De rien !

Bonne soirée à toi et bon travail