Probabilité - Variables discrètes

Bonjour,
J'ai un DS sur les probabilités. J'essaie de reprendre tous les TD mais je ne comprends strictement rien. De plus il n'y a eu aucune séance de cours étant donné que tout le monde avait étudié le chapitre pendant le lycée et la prépa (sauf moi )
Par exemple je ne sais pas faire le premier exo:

Les vaches laitieres sont atteintes par une maladie M avec la probabilité p=0,15 pour dépister la maladie M dan sune etable de n vaches, on fait proceder une analyse de lait. 2 méthodes possibles:

On fait une analyse sur un echantillon de lait de chaque vache
on effectue d'abord une analyse sur un échantillonde lait provenant du melange des n vaches. si le résultat est positif, au moins une des vaches est atteintes et on effectue donc une nouvelle analyse, cette fois pour chaque vache.

on veut connaitre la methode la plus economique ( c est a dire le moins d'analyse) pour cela on note Xn la variable aleatoire du nombre d'analyses réalisées dans la 2 eme étape. On pose Yn =Xn/n

determiner la loi de Yn. Tracer sa fonction de répartition et calculer son espérance.
etudier la fonction f(x) = ax+ln x, pour a = ln(0,85). donner la liste des entiers n tels que f(n)>0
Montrer que f(n)>0 equivaut à E(Yn)<1. conclure

Merci pour votre aide

Bonjour Raphael,

Je regarde la question 1)

PIstes,

$p (M) = 0.15$
$p (n o n M) = 1 - 0.15 = 0.85$

nonM veut dire "ne pas avoir la maladie."
On le nomme souvent $X‾\overline X$ donc on peut écrire $p(M‾)=0.85p(\overline M)=0.85$

Si aucune vache n'est atteinte de la maladie, $X_n=1$
$\times 0.85 \times...\times 0.85=(0.85)^n$

Evènement contraire
$p(X_n=1+n)=1-(0.85)^n$

$Yn=XnnY_n=\frac{X_n}{n}$
On utilise les résultats de $X_n$

Pour $\fbox{X_n=1}$, $\fbox{Y_n=\frac{1}{n}}$
donc $\fbox{p(Y_n=\frac{1}{n})=(0.85)^n} $

Pour $\fbox{X_n=1+n}$, $\fbox{Y_n=\frac{1+n}{n}}$
donc $\fbox{p(Y_n=\frac{1+n}{n})=1-(0.85)^n}$

Pour l'espérance, utilise la formule usuelle
$E(Yn)=1n(0.85)n+n+1n(1−(0.85)n)E(Y_n)=\frac{1}{n}(0.85)^n+\frac{n+1}{n}(1-(0.85)^n)$

Commence à voir cela .

Reposte si tu as besoin pour la suite.

Bonjour et merci de votre réponse.

quand vous dites "élément contraire" cela veut dire toutes les vaches sont atteintes de la maladie?
Ensuite pourquoi p(Xn=1) = 0,85^n ?

et enfin pour l'espérance c'est une régle? ça représente quoi?

Merci

Pour une vache donnée, M veut dire "avoir la maladie" et "nonM" veut dire "ne pas avoir la maladie"

$X_n=1$ correspond au cas où aucune vache n'est atteinte par la maladie, c'est à dire le cas où l'évènement "nonM" se produit n fois (avec chaque fois la probabilité 0.85)
Calcul : "nonM" suivi de "nonM"...suivi de "nonM" (n fois) a la probabilité $0.85 \times 0.85\times...\times 0.85$ (n fois), c'est à dire $0.85^n$

L'évènement contraire à "aucune vache n'est atteinte de la maladie" est "au moins une vache est atteinte de la maladie"

L'espérance représente une "moyenne". C'est une définition que tu dois trouver dans ton cours (c'est une formule à appliquer)

Xn parce que 1-0=1 mais dans ce cas on ne peut pas réutiliser le 0,85?

Je ne comprends pas trop ce "1-0"...
Le cas $X_n=1$ correspond au cas où aucune vache est malade , c'est à dire au cas où on ne fait qu'une seule analyse (d'où la valeur 1 pour $X_n$ )

Oui...on utilise le 0.85 n fois ( car l'évènement "nonM" est réalisé n fois ( car aucun vache est malade ; elles sont toutes "non Malades")

D'accord je comprends mieux par contre je ne comprends pas les 2eme resultat pour donc encadré comment les trouver?

Désolée, mais je ne comprends pas ce que tu veux dire par ..
les 2eme resultat pour donc encadré comment les trouver?

???

Tu parles de quoi ?
Du second cas de la première question où la première analyse donne un résultat positif (c'st à dire lorsque au moins une vache est malade) ou de la seconde question où tu dois étudier la fonction f ?

Merci de clarifier ta question.

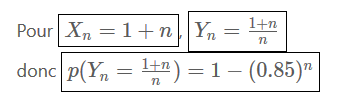
Je parlais de ces résultats que je ne comprends pas.
Est ce que l'événement contraire sera toujours 1+n? (ou cela dépend de l'exercice)
Pour l'événement contraire, il est noté 1+n par contre vous faite 1-(0,85)^n
Merci

Il s'agit donc de la question1.
C'est l'évènement contraire qui te pose problème.

Il faut comprendre l'énoncé .
Sans comprendre l'énoncé, surtout en probabilité, on ne peut rien faire.
Il est écrit:
"on effectue d'abord une analyse sur un échantillon de lait provenant du mélange des n vaches. si le résultat est positif, au moins une des vaches est atteintes et on effectue donc une nouvelle analyse, cette fois pour chaque vache"

Je vais essayer de faire de l'explication du texte.

Dans le cas où le résultat est négatif lors de la première analyse (analyse sur l'échantillon des laits mélangés) , cela veut dire qu'aucune vache n'est malade.
On ne fait pas d'autres analyses donc le nombre d'analyse est 1 donc $X_n=1$ et la probabilité est $0.85)^n$ (déjà expliqué)

Dans le cas où où le résultat est positif lors de la première analyse (analyse sur l'échantillon des laits mélangés), cela veut dire que au moins une vache est malade.et on fait alors une analyse supplémentaire par vache.
Cela fait donc une analyse + n analyses (vu qu'il y a n vaches) :
Total du nombre d'analyses =1+n
donc $X_n=1+n$
Cet évènement étant contraire au précédent, la probabilité vaut "1 moins la probabilité précédente", c'est à dire $1-(0.85)^n$

J'écrivais mon explication sur $X_n$ (longue explication;;;) alors que tu modifiais ta demande.et que tu indiquais qu'il s'agissait de $Y_n$ ! ! !
Je l'ignorais...
Tu devrais éviter de modifier ta demande avant d'avoir une réponse...car on s'y perd !

Si tu as compris $X_n$ , il n'y a rien à faire de particulier sur $Y_n$
Tu divises simplement $X_n$ par n
Les probabilités sont inchangées vu qu'il s'agit de la même expérience aléatoire. Il s'agit seulement d'un changement de variable.

Merci Mtschoon, je pense avoir compris ce qui ne marchait pas. J'essaie de refaire la première question.

Tout à fait.
Il faut assimiler la première question qui est spécifique aux probabilités.

Les questions 2. et 3. sont, en fait, des questions sur étude de fonction et calculs usuels.

J'ai repris la première question qui est dès à présent plus clair.
Par contre je ne vois toujours pas comment déduire quelle solution est la plus économique.

La conclusion pour savoir quelle solution est la plus économique s'obtient après avoir fait les questions 2 et 3.
$E(Yn)<1E(Y_n) \lt1$ <=> $\gt 0$
Pour les valeurs de n satisfaisant à $\gt 0$ , on a intérêt à choisir la seconde méthode.

Il faut donc avoir fait les questions 2 et 3.pour pouvoir conclure.

Indique tes réponses à ces questions, si besoin.

Merci beaucoup

De rien ! Bon travail.