Exercice Stat - Les classes (Corrections)

Bonjour,
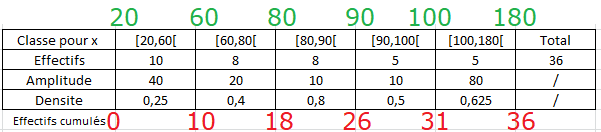
J'ai besoin d'une petite correction relative à mon exercice en Stat. Je dois me baser sur le tableau ci-dessous et trouver la valeur médiane, le 1er quartile, 3eme quartile, l'interquartile.

Pour trouver la valeur de la médiane:
ME = 80 (0 / 8 de 20) = 80
1er quartile
Q1 = 20 + 9 / 10 de 40 = 56
3eme quartile:
Q3 = 90 + 1 / 5 de 10 = 92
Interquartile:
92 - 56 = 36

Est-ce que mes formules vous semble être correctes c'est celles du cours.

Ah, oui je dois aussi trouver l'étendue de cette distribution par contre là je comprends pas. Je dois me baser sur les effectifs non ? Mais il y a deux classes qui ont 5 effectifs ??

Bonjour Augustin,

Tout est bon pour tes 4 réponses.

L' étendue c'est la différence entre les valeurs extrêmes.
L’étendue de la série est donc de 180 – 20 = 160
Cette information n’a pas grand intérêt avec une série répartie en classes, car on ignore comment les bornes extrêmes ont été choisies...

Bonjour Mtschoon

Merci pour tes corrections et tes explications. Je dois maintenant représenter cela dans deux graphiques.

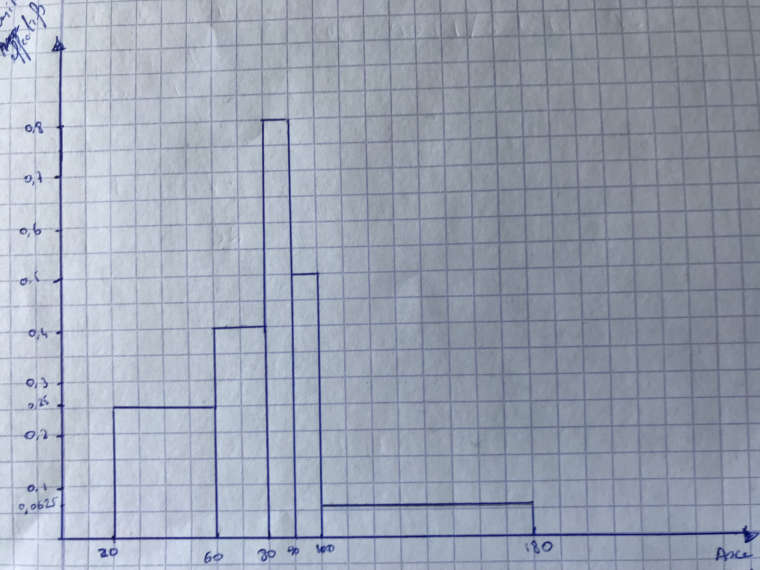
L'histogramme (le voici)

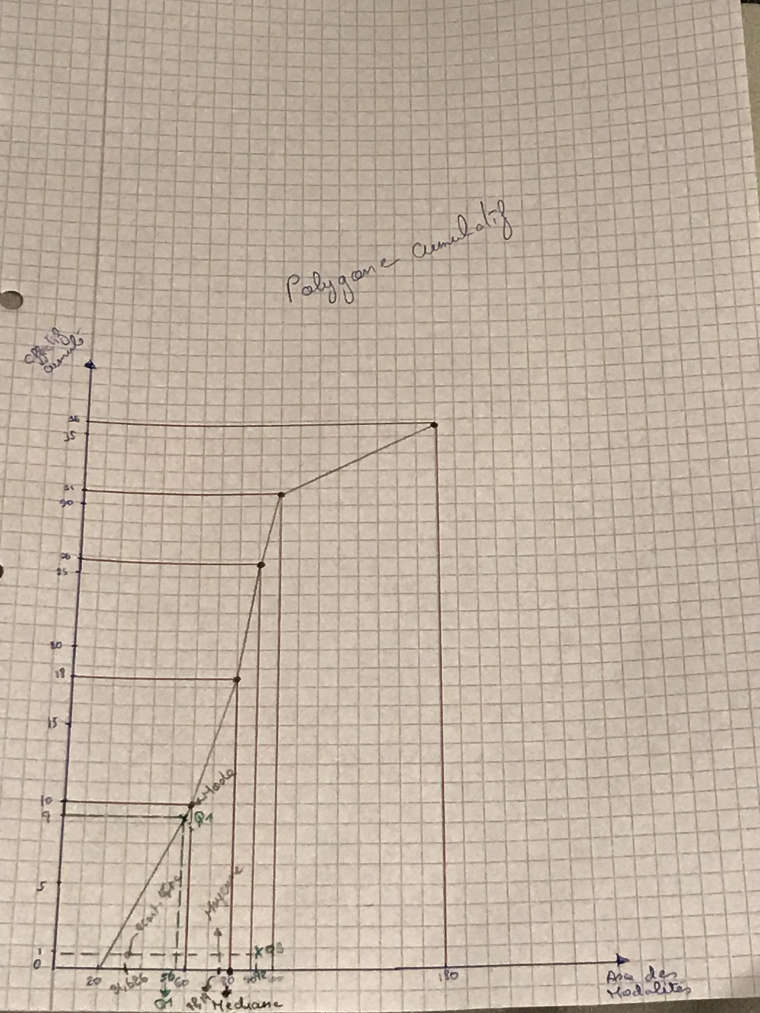
Polygone Cumulatif
je dois inclure la médiane, le 1er quartile et le troisième quartile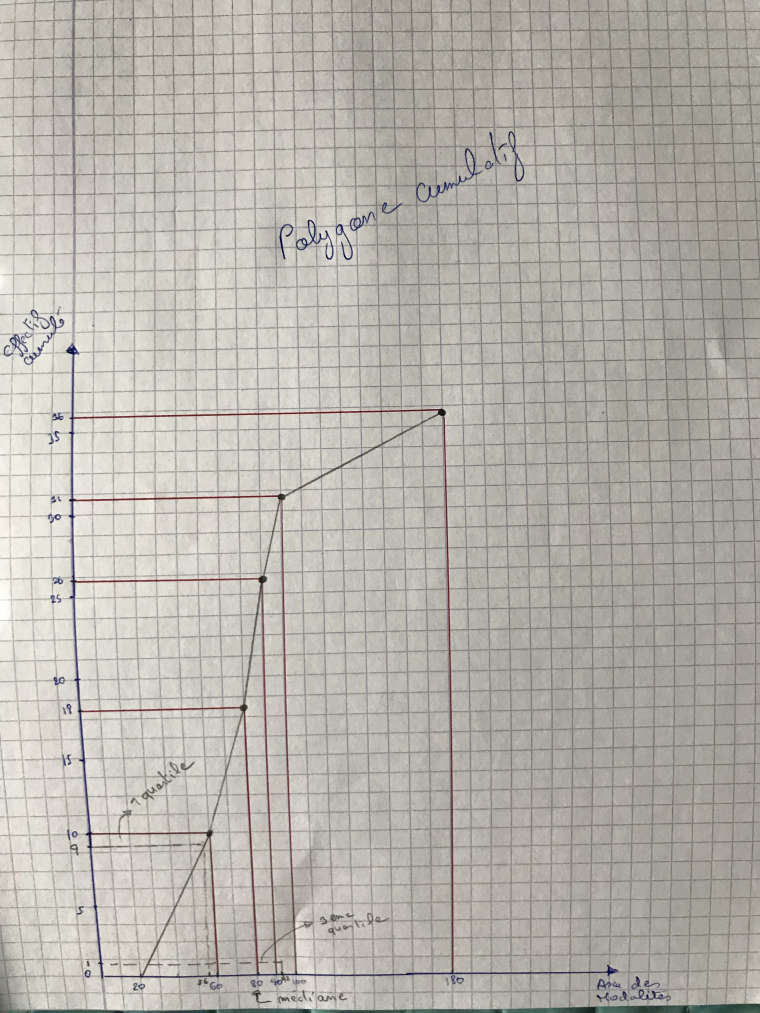

Est-ce que cela te semble plus ou moins corrects ?
ps: désolé si c'est pas super lisible...

Les "graphiques" sont bons .

Pour l'histogramme, je pense que, pour l'axe des abscisses, tu as marqué "axe des modalités" mais on ne le voit pas.
Pour l'axe des ordonnées, tu as utilisé les densités donc nomme cet axe "axe des densités"
(Si tu avais utilisé les effectifs, il aurait fallu écrire "axe des effectifs")

Pour le polygone cumulatif, le schéma est bon
Q1, ME et Q3 doivent être mis en valeur.
Je pense que c'est ce que tu as fait mais on voit mal Q3.
Q1=56 il correspond à 25% de l'effectif total , c'est à dire à 9
ME=80 il correspond à 50% de l'effectif total , c'est à dire à 18
Q3=92 il correspond à 75% de l'effectif total , c'est à dire à 27

Tu as bien travaillé !

Bonsoir Mtchoon,
Merci pour ton retour. Effectivement pour l'histogramme c'est bien "axe des modalités" mais la photo a mal été prise. En revanche dans mon cours pour l'axe des ordonnées on le nomme "densité d'effectifs" mais je vais mettre "axe des densités".

Il faut maintenant que je repère dans mon graphique, la moyenne, l'écart-type, le mode. J'ai utilisé ce tableau !

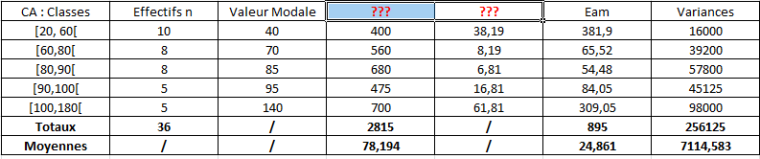
1/ dans les titres des colonnes; il me manque deux titres, comment je pourrais les nommer?
2/ la moyenne = 78.194 | écart-type = 31.626
3/ le mode est 10; car c'est la valeur observée la plus fréquente

Il faut maintenant que je remette ceci sur mon graphique précédent.
J'ai écrit au crayon dans le même graphique où se situait le mode, la moyenne et l'écart-type; je sais que c'est pas super précis/propre désolé..

ou bien celui-ci

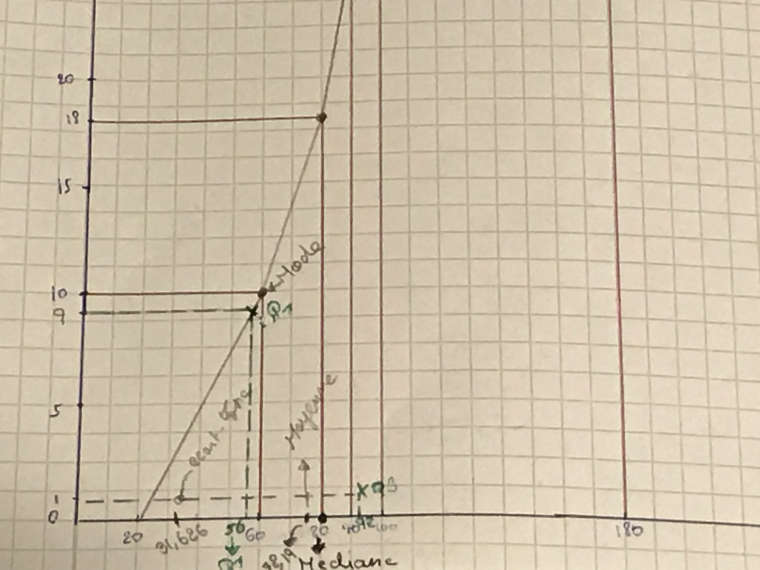
ps: qu'est-ce que ça veut dire "tirer des minorantes pour l'écart-type" ??

Un grand merci pour ton retour.

Bonjour Augustin,

Ce que te dit ton cours sur l'axe des ordonnées est très bien.

Tu peux écrire "axe des densités d'effectifs" vu que c'est de cela qu'il s'agit.
Utilise impérativement de terme "densités" vu que tu as utilisé les densités pour les ordonnées.
Les densités sont les densités calculées avec les effectifs, donc préciser "densités d'effectifs" est parfait.

Je regarde tes questions 1),2),3).

1.Pour le titre de la colonne en bleu, tu peux mettre Moyenne, vu que cette colonne calcule la moyenne de la série.
Elle calcule les produits des centres des classes par les effectifs correspondants, elle les ajoutent et enfin elle divise par l'effectif total pour trouver obtenir la moyenne 78,194

Pour le titre de la colonne en bleu, tu peux mettre Ecarts vu que cette colonne calcule les écarts entre les centres des classes et la moyenne :
|40 - 78,194| = 38.194 , |70 - 78,194| = 8.194 , etc,...

J'espère que tu es d'accord sur l'Eam de la cinquième colonne.
Cette colonne calcule les produits des écarts par les effectifs correspondants, elle les ajoute et enfin elle divise cette somme par l'effectif total pour obtenir l'Eam de 24.861

Une remarque : pour le titre de la dernière colonne j'aurais mis "Variance" au singulier et non au pluriel...
Cette colonne calcule les carrés des écarts, les ajoutent et enfin elle divise cette somme par l'effectif total pour trouver la Variance qui vaut 7114.583

2.Oui pour la moyenne.

Je ne vois vraiment comment tu trouves la valeur de l'écart-type
L'Ecart-type est la racine carrée de la Variance
L'Ecart-type vaut donc $7114.583=84.348\sqrt{7114.583}=84.348$

3.Tu as dû faire une confusion.
L'effectif le plus fréquent est 10.
Le mode est donc la valeur 40 'c'est la "valeur modale" (d'où le titre de la troisième colonne)

Ce serait bien que tu regarde tout cela de près.

Rectifie les graphiques en fonction des corrections apportées.

Bonsoir Mtschoon,

Merci beaucoup pour toutes tes explications précises (comme toujours).
Voici mon nouveau graphique brouillon pour le mode, je pense que c'est maintenant correct ?
J'ai une autre petite question, que signifie "tirer des minorantes pour l'écart-type" ??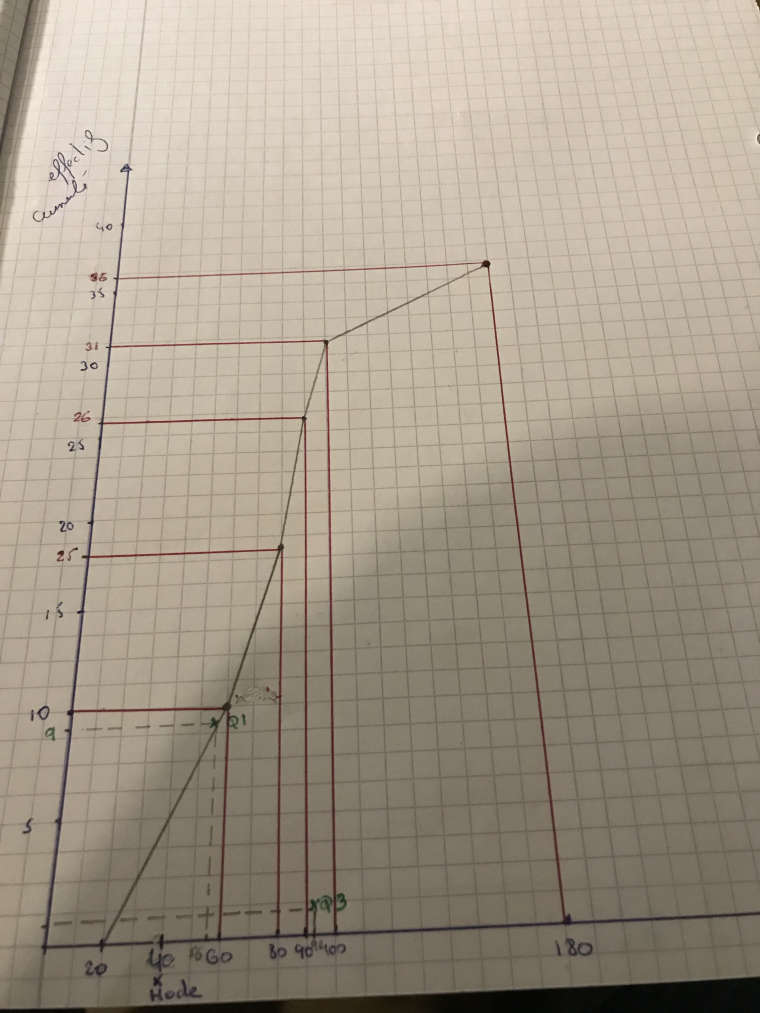

Bonne soirée

Oui, ton graphique me parait correct.

La formulation "tirer des minorantes pour l'écart-type" me laisse un peu perplexe...mais ce n'est pas la première fois que l'on voit des différences d'expressions entre Belgique et France...

Une explication .

La valeur exacte de l'écart-type est $7114.583\sqrt{7114.583}$

Cette valeur est un nombre irrationnel.
Son développement décimal est illimité et non périodique.
Il est donc impossible de connaître toutes les décimales exactes.

84.384, que je t'ai indiqué, est une valeur approchée donnée par une calculette.
Si tu élèves cette valeur au carré, tu constateras que son carré est légèrement supérieur à 7114.583
Donc 84.348 est une valeur approchée par excès de l'écart-type : c'est une valeur majorante)

En prenant 84.347 et en l'élevant au carré, tu constateras que son carré est légèrement inférieur à 7114.583
Donc 84.347 est une valeur approchée par défaut de l'écart-type : c'est une valeur minorante)

Remarque :

Si tu prends un calculateur très perfectionné (trouvé sur le web), tu pourras obtenir 84.3479934556833
Cela est une valeur approchée (très précise) par défaut : c'est une valeur minorante

Avant les ordinateurs et calculatrices, on calculait les valeurs approchées des racines carrées "à la main" en faisant une disposition pratique ressemblant à la disposition pratique des divisions.
On obtenait ainsi
84 puis 84.3, puis 84.34, puis 84.347 puis 84.3479, etc...
Toutes ces valeurs sont des valeurs minorantes de $7114.583\sqrt{7114.583}$

Tu dois donc donner quelques unes de ces valeurs.

(Evidemment, toutes les valeurs inférieures à 84 sont aussi des valeurs minorantes, mais elles me semblent n'avoir aucun interêt)

Bonjour Mtschoon,

Je ne connaissais vraiment pas tout ça, merci beaucoup pour toutes tes explications, je vais les noter dans mes notes de cours.

Bonjour Augustin,

J'espère t'avoir indiqué un complément utile à ton cours.
Bonne lecture !