Score Z en probabilité (loi normale réduite centrée)
-
AAugustin dernière édition par mtschoon
Bonjour,
J'aimerais bien apprendre à savoir calculer la note Z qui permet de situer l'individu par rapport aux autres. Admettons que nous avons dans un exercice ceci:On cherche à connaître le point fort dans un service d'un hôtel et son point faible. Pour cela on a attribué 4 notes qui sont : 8 6 4 2
Pour calculer la Note Z on aura besoin de la moyenne de chaque service et de l'écart-type d'après ce que j'ai compris?
Accueil => 8,5 (m) => 12 σ
Service => 12.30 (m) => 4.2 σ
Propreté => 425 (m) => 165 σ
Cuisine => 48 (m) => 18 σPour l'Accueil j'ai ceci
La note 8 :
8 - 8.5 = -0.5
-0.5 est à 0.5 de la moyenne
0.5 / 12 = 0.042La note 6:
6 - 8.5 = -2.5
2.5 / 12 = 0.208La note 4:
4 - 8.5 = -4.5
4.5 / 12 = 0.375La note 2:
2 - 8.5 = -6.5
6.5 / 12 = 0.542Est-ce que c'est bien comme cela qu'il faut s'y prendre ?
-
mtschoon dernière édition par mtschoon

Bonjour Augustin.
Oui, c'est bien ainsi qu'il faut s'y prendre mais il faut conserver le signe.
X étant une variable aléatoire de valeurs xix_ixi suivant une loi (approximativement) normale , Z est la loi normale réduite centrée associée.
$\fbox{Z=\frac{x_i-m}{\sigma}}$
Z a pour moyenne 0 et pour écart-type 1Pour la note 8, Z=-0.042
cette note est ainsi à 0.042 écarts-type de la moyenne, en dessous.Idem pour les autres notes
Pour la note 6, Z=-0.208
Pour la note 4, Z=-0.375
Pour la note 2, Z=-0.542
C'est notes (en Z) étant négatives, elle sont toutes en dessous de la moyenne.
Bien sûr, plus l'écart (en valeur absolue) est grand, plus la note est mauvaise.Si les notes (en Z ) étaient positives, elles seraient au dessus de la moyenne.
Plus l'écart (en valeur absolue) serait grand, plus la note serait bonne.Je te mets un lien vers une explication du "Sore Z" qui pourra peut-être t'interésser.
https://psychometrie.espaceweb.usherbrooke.ca/score-zBonne lecture et bon travail.
-
AAugustin dernière édition par
Bonjour Mtschoon,
Je te remercie pour toutes explications. J'ai fait tous les calculs, je dois maintenant additionner toutes les notes Z de chaque service et ensuite les comparer aux autres?
Donc l'Accueil j'aurais par exemple -0.042 + -0.208 + -0.375 + -0.542 = -1.167Pour l'Accueil j'ai ceci :
m = 8.5 et σ 12Pour la note 8 :
8 - 8.5 = -0.5
-05 / 12 = -0.042Pour la note 6 :
6 - 8.5 = -2.5
-2.5 / 12 = - 0,208Pour la note 4:
4 - 8.5 = -4.5
-4.5 / 12 = - 0.375Pour la note 2:
2 - 8.5 = -6.5
-6.5 / 12 = -0542Pour le Service j'ai ceci :
m = 12,30 et σ 4.2Pour la note 8 :
8 - 12.30 = -4.30
-4.30 / 4.2 = -1.024Pour la note 6 :
6 - 12.30 = -6.3
-6.3 / 4.2 = - 1.50Pour la note 4:
4 - 12.30 = -8.30
-8.30 / 4.2 = - 1.976Pour la note 2:
2 - 12.30 = -10.30
-10.30 / 4.2 = -2.452Pour la Propreté j'ai ceci :
m = 425 et σ 165Pour la note 8 :
8 - 425 = -417
-417 / 165 = -2.527Pour la note 6 :
6 - 425 = -419
-419 / 165 = - 2.540Pour la note 4:
4 - 425 = -421
-421 / 165 = -2.552Pour la note 2:
2 - 425 = -423
-423 / 165 = -2.564Pour la Cuisine j'ai ceci :
m = 48 et σ 18Pour la note 8 :
2- 48 = -46
-46 / 18 = -2.555Pour la note 6 :
6 - 48 = -42
-42 / 18 = - 2.333Pour la note 4:
4 - 48 = -44
-44 / 18 = -2.444Pour la note 2:
2 - 48 = -46
-46 / 18 = -2.555
-
mtschoon dernière édition par mtschoon

Tes calculs me semblent satisfaisants.
Si ce n'est pas déjà fait, je te conseille de faire ensuite un tableau récapitulatif pour clarifier la situation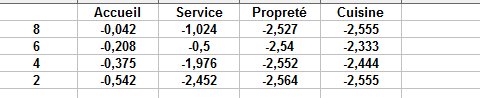
Si cet énoncé correspondait à des valeurs réelles, tu aurais des scores Z un peu plus variés (situés la plupart du temps entre -3 et +3 alors qu'ici ils sont tous négatifs, mais bien sûr, il s'agit ici seulement d'un exemple.
Pour tirer ensuite une conclusion sur la comparaison des services, je doute de ta méthode.
Tu ne fais intervenir que les scores sans tenir compte des notes.
J'aurais l'idée de faire des combinaisons" notes avec scores" pour obtenir une valeur indicatrice de chaque service et comparer ensuite ces valeurs indicatrices trouvées.
Plus la valeur indicatrice sera élevée, plus le service concerné sera bon.Accueil : [8×(−0.042)]+[6×(−0.208])+[4×(−0.375)]+[2×(−0.542])[8\times (-0.042)]+[6\times (-0.208])+[4\times (-0.375)]+[2\times(-0.542])[8×(−0.042)]+[6×(−0.208])+[4×(−0.375)]+[2×(−0.542])
Tu comptes
Service :
[8×(−0.024])+[6×(−1.5)]+[4×(−1.976)]+[2×(−0.452)][8\times (-0.024])+[6\times (-1.5)]+[4\times (-1.976)]+[2\times(-0.452)][8×(−0.024])+[6×(−1.5)]+[4×(−1.976)]+[2×(−0.452)]
Tu comptes
Même principe pour Propreté et Cuisine.Tu pourrais ensuite ajouter une ligne au tableau pour compléter avec ces valeurs indicatrices.
Regarde la méthode indiquée dans ton cours, car l'idée que je te propose est personnelle, et j'ignore si c'est la pratique usuelle...
-
mtschoon dernière édition par mtschoon

Pour clore ce topic, voici les conclusions tirées en utilisant les valeurs indicatrices proposées.
Sauf erreur,
Accueil : -4.168
Sevcice : -17.096
Propreté : -50.792
Cuisine : -49.324Dans l'ordre, l'Accueil est la meilleure des prestations, suivie du Service, puis de la Cuisine et enfin de la Propreté.
Evidemment, tout cela reste dans le négatif....
-
AAugustin dernière édition par
Bonsoir Mtschoon,
Un très grand merci pour tes explications, j'ai maintenant compris les étapes à réaliser pour pouvoir déterminer le service le plus efficace. Je vais prendre note de toutes tes explications et de ton tableau qui facilite les calculs.
Je vais maintenant m'entraîner avec d'autres exercices du même style , on peut clôturer ce topic encore 1000 fois merci pour le temps que tu as consacré à me répondre.
Bonne soirée
-
mtschoon dernière édition par mtschoon

De rien Augustin et bonne fin pour cette année scolaire.

-
mtschoon dernière édition par mtschoon

Un grand Merci Augustin pour ton gentil message privé reçu ce jour, et encore toutes mes félicitations pour ton succès


