Matrice - Diagonalisation / Valeurs propres

Bonjour, j'ai besoin d'un petit coup de pousse.
Je cherche à savoir si la matrice:
2 1 -1
2 2 -2
1 1 0
est diagonalisable?
Si j'ai bien compris elle est diagonalisable si je trouve 3 valeurs propres distinctes.

Après calculs je trouve -x^3+4x^2-5x+2 à partir de là quelle est la méthode pour trouver les valeurs propres.

Merci par avance pour votre coup de pouce

Re-bonjour Dut,

Effectivement, si tu trouves 3 valeurs propres distinctes, tu pourras conclure que la matrice est diagonalisable, mais attention, la réciproque n'est pas vraie !
Une matrice diagonalisable peut avoir des valeurs propres distinctes ou pas...
En bref, si les 3 valeurs propres ne sont pas toutes distinctes , il faut continuer le travail avec les vecteurs propres pour pouvoir tirer une conclusion.

Pour le petit coup de pouce que tu demandes :

Les valeurs propres seront les solutions de l'équation caractéristique $\fbox{-x^3+4x^2-5x+2=0}$

Tu dois donc résoudre cette équation.

Bons calculs .

Bonjour Mtschoon,
Pour résoudre il faut utiliser le discriminant? normalement en utilisant le discriminant il n'y a que 3 valeurs nommées a, b et c, dans ce cas il faut rajouter d?

Non...

Le discriminant est utilisé pour les équations du second degré.

L'équation que tu as à résoudre est du troisième degré

Il existe bien des formules très compliquées ( avec racines cubiques ) pour le troisième degré (méthode de Cardan), mais elles ne sont guère utilisées et tu ne dois pas les connaître.

Dans ce type d'équation, usuellement, il y a une (ou plusieurs) solutions dites "évidentes" que l'on trouve en "testant".
On teste habituellement 0 , 1 ,-1, 2,-2.
Si l'énoncé est bien fait, une ou plusieurs valeurs doivent être solutions de l'équation. Ensuite, il faut terminer la résolution.
Regarde ton cours.Tu as dû voir cela.

Merci alors dans mon cours il n'utilise pas la méthode de Sarrus mais le développement d'une ligne ou d'une colonne avec factorisation pour éviter de se retrouver dans cette situation.
J'ai essayé les solutions "dites évidentes" je trouve 1 et 2.
1 et 2 sont donc les valeurs propres?

Oui 1 et 2 sont bien des valeurs propres mais il faut savoir si se sont les seules.
Il y a différentes méthodes : factorisation, identification, division euclidienne,... Fais comme tu as l'habitude.

En factorisant, l'équation caractéristique peut s'écrire : $2-x)(x-1)^2=0$

Conclusion : les seules valeurs propres sont 1 et 2
2 est valeur propre simple
1 est valeur propre double

Oui là je vois. Néanmoins j'ai un problème de niveau 3ème je n'ai aucune méthode pour factoriser d’autant plus qu'il y a une identité remarquable.
A part essayer et vérifier en faisant le calcul après ( ce qui peut prendre 5 minutes avec de la chance ou beaucoup beaucoup plus) je ne sais pas factoriser

J'explicite un peu

Raisonne logiquement.

1 est solution de l'équation donc on peut mettre (x-1) en facteur
2 est solution de l'équation donc on peut mettre (x-2) en facteur

Vu que l'équation est du 3ème degré, le 3ème facteur sera du premier degré
L'équation s'écrira :
(x-1)(x-2)(ax+b)=0

Bien sûr, tu peux maintenant développer et identifier avec l'écriture de départ, pour trouver a et b mais c'est long...

Le plus rapide est de raisonner encore.
$x^3$ s'obtient par le produit des termes $x×x×axx\times x \times ax$ , pour tout x
Tu déduis que a=-1
+2 s'obtient par le produit des termes $−1×−2×b-1\times -2 \times b$
Tu déduis que b=1

Conclusion :
L'équation s'écrit $(x-1)(x-2)(-x+1)=0\fbox{(x-1)(x-2)(-x+1)=0}$
Les solutions sont donc x=1, x=2 x=1, c'est à dire : 2 est solution simple et 1 est solution double.

Pour faire plus "esthétique", tu peux transformer, mais ce n'est pas indispensable.
En changeant les signes des deux derniers facteurs (ce qui ne change pas le résultat final)
$(x - 1) (- x + 2) (x - 1) = 0$ <=> $\fbox{(-x+2)(x-1)^2=0}$ <=> $\fbox{(2-x)(x-1)^2}=0$

CQFD

Une remarque,

En appelant A la matrice et I la matrice identité

Tu as développé Det(A-xI) en totalité et ainsi tu as obtenu une expression du 3ème degré.
C'est exact, mais tu aurais pu avoir une factorisation directe par (2-x) qui aurait été bien plus simple...

En développant le déterminant Det(A-xI) avec la première ligne, sans tout développer, tu peux obtenir
$2-x)(-2x+x^2+2)+(x-2)=(2-x)(-2x+x^2+2-1)$

En simplifiant, tu obtiens $2-x)(x^2-2x+1)$

En reconnaissant une identité remarquable, tu obtiens $\fbox{(2-x)(x-1)^2}$

C'est vraiment plus facile...

Bonsoir Mtschoon, merci pour cette explication que je reprendrai tranquillement demain étant cloué au lit car malade
Vu qu'il y a 3 valeurs dont une double la matrice est diagonalisable ?
Bonne soirée

Dans ce cas, comme je te l'ai indiqué, tu ne peux pas conclure à ce stade, vu que les 3 valeurs propres ne sont pas distinctes.
Il faut étudier les vecteurs propres pour pouvoir tirer une conclusion.

Bien sûr, soigne toi d'abord, tu verrais tout cela ensuite, lorsque tu auras retrouvé la forme .

Bonjour,
J'ai essayé de trouver les vecteurs propres. Pour ce faire je pose

la matrice A * les inconnues que je nomme X = les résultats que je nomme B

2 1 -1 x 1
2 2 -2 * y = 1 (La valeurs propre que nous avons trouvé)
1 1 0 z 1

Pour résoudre X on fait x=A^-1 *B

J'ai calculé A^-1:
1 -1/2 0
-1 1/2 1
0 -1/2 1

Enfin pour conclure x=y=z=1/2 est ce c'est la bonne méthode?
Merci

Bonjour,
Je ne comprends guère ta méthode .

Soit :
A la matrice à traiter
$λ\lambda$ une valeur propre
$I_3$ la matrice identité

Les vecteurs propres ( $x_1,x_2,x_3)$ de $R^3$ associés à la valeur propre $λ\lambda$ se définissent par :

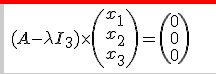
0_1534165834523_9683bb3c-9f90-4dd6-9cd5-6b2e6f2a338a-image.png

Tu dois savoir que ces vecteurs propres forment un SEV de $R^3$

Donc :
Tu remplaces $λ\lambda$ par 1 et tu développes la formule surlignée de rouge.
Tu obtiens un système d'inconnues $x_1,x_2,x_3$ qui te permet d'avoir la nature de ce SEV , noté $E_1$ , et sa dimension

Tu fais pareil pour $λ=2\lambda=2$ et tu obtiens la nature et la dimension de ce SEV noté $E_2$

Par théorème, vu que dim( $R^3$ )=3 :
si dim( $E_1$ )+dim( $E_2$ )=3, alors A est diagonalisable
si dim( $E_1$ )+dim( $E_2$ ) $≠\ne$ 3, alors A n'est pas diagonalisable

Bons calculs.

J'obtiens comme matrice:

1. -1
1. -2
1. -1
  Après résolution:
  X=0
  Y=0
  Z=x+y

C'est ce que vous attendiez ?

Oui pour la matrice A- $I_3$

Ensuite, il faut multiplier par la matrice colonne
$x_1$
$x_2$
$x_3$
Ecrire que le résultat est
0
0
0

Tu dois , sauf erreur, trouver le système
$x_1+x_2-x_3=0$
$2x_1+x_2-2x_3=0$
$x_1+x_2-x_3=0$

Tu analyses ce système pour tirer la conclusion sur $E_1$

Bonjour Mtschoon, c'est bien ce que j'ai trouvé et ce que je vous ai indiqué dans le précédent message, je n'avais juste pas mis z=0 mais z=x+y mais étant donné que x et y=0 cela revient au même.
Ma conclusion est que le vecteur propre est (0,0,0) pour la valeur propre 1. Cette valeur propre étant double on voit bien que le vecteur sera toujours (0,0,0) de ce fait pour dire que la matrice est diagonalisable il faudrait 2 vecteurs distincts pour lambda=1. La matrice n'est donc pas diagonalisable.

Revois ta dernière explication...

Si tu résous ce système correctement, tu dois pourvoir trouver que $x_2=0$ et $x_1=x_3$

$E_1$ est composé des vecteurs de la forme
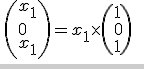
0_1534237522405_2f4b6b38-d18a-457f-ae4a-fbe0255410e1-image.png

$E_1$ est donc une droite vecoreille de base ( $1, 0, 1)$
dim $E_1)=1$

Lorsque tu as compris cela, tu traites $E_2$

Alors je trouve bien x1=x3 ; x2=0 et x3=x1
Donc le vecteur propre est (1, 0, 1) mais pourrait très bien être (2,0,2) on est d'accord?
Comment vous savez que dim(E1)=1

E2 est la 2ème valeurs propre soit 2?
Après on détermine la diagonalisation suite au théorème que vous m'avez donné plus haut

Il y a une infinité de vecteurs propres associés à $λ=1\lambda=1$
(2,0,2) en est un autre bien sûr et ( $k, 0, k)$ en général, avec k appartenant à R.

Comme déjà indiqué, ces vecteurs forment un SEV de $R^3$
Tous ces vecteurs propres sont" multiples" de (1.0.1) qui constitue une base de ce SEV.
Comme cette base a un seul élément, dim( $E_1$ )=1
Il s'agit d'une droite vectorielle.

C'est dommage que tu n'aies pas rencontré de droite vectorielle dans ton exercice précédent car tu comprendrais mieux ici.

Tu as à passer maintenant à $λ\lambda$ =2

Pour E2
La matrice associée est:
0 1 1
2 0 -2
1 1 -2

En résolvant (je ne suis pas sûr,le résultat me paraissant bizarre)
Z=(x+y)/2
Y=0
X=0

Revois la première ligne de la matrice : c'est 0 1 -1

Pour le système obtenu, les inconnues sont $x_1 , x_2, x_3$

Tu dois répondre en fonction de ces inconnues.
Je ne vois pas ce que sont ces x,y,Z...

Si besoin, indique tes calculs pour pouvoir comprendre où se situent ces "bizarreries".

Alors en utilisant les mêmes notation je trouve:
x3=(x1+x2)/2 puis en remplaçant x1 et x2 je trouve au final x3=x3

x1=x3
x2=x3
Si cela n'est pas juste je vois envoie tous les calculs pour en arriver à cette conclusion

C'est bon
Il te reste à tirer les conclusions sur $E_2$

Merci.
Je pense que j'en n'ai pas assimilé les dimensions.
Mais je dirais que x3 entraîne x1 et x2 donc la dimension est 1

C'est un peu ça, mais pour l'explication, il faut améliorer...

Vu que $x_1=x_2=x_3$ , tu peux exprimer en fonction d'une seule variable, par exemple $x_1$
L'ensemble des vecteurs propres est donc composé des vecteurs:

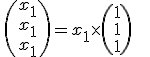
Tous ces vecteurs propres sont" multiples" de (1.1.1) qui constitue une base de ce SEV $E_2$
Comme cette base a un seul élément, din( $E_2$ )=1
Il s'agit d'une droite vectorielle.

Et vu dim(e1)+dim(e2)=2#3 la matrice n'est pas diagonalisable.
Autre petite précision on parle depuis le début des R^3 c'est parce que c'est une matrice 3x3?

Oui !

Si tu as le temps, je te conseille de revoir ton cours pour bien maitriser ces notions.

Si ton cours n'est pas clair, je te mets un lien qui pourra peut-être t'intéresser.

Evidemment, il faut prendre le temps pour l'approfondir !

https://openclassrooms.com/fr/courses/1263156-techniques-pratiques-de-diagonalisation-dune-matrice

Bon travail !

Oui je vais reprendre ça attentivement.
merci beaucoup Mtschoon pour votre aide c'est beaucoup plus clair et j'ai surtout toutes les étapes.

De rien Dut !

A+