Matrices - Noyau, image, polynôme minimal

Bonjour,
Pouvez-vous m'indiquer les étapes pour la réalisation de cet exercice:
soit A=
-2 0 0
0 -1 -1
0 -1 -1

Décrire le noyau ker(A) et l'image Im(A) de la matrice A, c'est à dire: donner une base de chacun de ces sous-espaces vectoriels de R^3.
Calculer le polynôme minimal Ma de A (Question qui revient régulièrement dans ce sujet mais dont je n'ai qu'un exercice similaire sur les TD qui n'a pas été corrigé)

Merci pour votre aide et tous vos conseils

Bonjour,

Je regarde ta première question.

A est la matrice d'une application linéaire f de $R^3$ vers $R^3$ (endomorphisme de $R^3$ )

Le noyau de f se note habituellement Ker(f)
Ker(f) est l'ensemble des vecteurs (x,y,z) de $R^3$ (ensemble de départ) tels que :

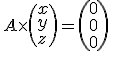
Après calculs, tu dois trouver le système :
$2 x = 0$
$- y - z = 0$
$- y - z = 0$
Les vecteurs de Kerf peuvent donc s'écrire:

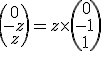
Kerf est donc le SEV de $R^3$ de base (0,-1,1)
Kerf est la droite vectorielle de base (0,-1,1)
$dim(Kerf)=1\fbox{dim(Kerf)=1}$

L'image de f se note habituellement Im(f)
C'est l'ensemble de vecteurs (X,Y,Z) de $R^3$ (ensemble d'arrivée) ayant au moins un antécédent (x,y,z) dans $R^3$ (ensemble de départ) par f.
C'est encore un SEV de $R^3$

Le plus simple est le passer par le "théorème du rang" :
$\fbox{dim(Kerf)+dim(Imf)=dim(R^3)}$ (ensemble de départ)

Tu trouves ainsi directement $dim(Imf)=2\fbox{ dim(Imf)=2}$
Imf est donc un plan vectoriel

Pour donner une base de Imf, il te suffit de choisir 2 vecteurs colonnes non colinéaires de la matrice A
Ici, tu peux donc prendre (2,0,0) et (0,-1,-1)

Regarde cela de près.

Si tout cela te convient, je te donnerai ensuite des indications sur la question 2 relative au polynôme minimal.
Cette seconde question n'a rien à voir avec la question 1 vu qu'elle est liée au polynôme caratéristique,aux valeurs propres et a aussi un lien avec la diagonalisation éventuelle de la matrice.

Bonjour Mtschoon,
Merci pour votre première explication que je pense avoir compris. Néanmoins j'aimerais approfondir deux petits points.
1er point: Tout d'abord l'écriture du vecteur kerf.
Après résolution:
x=0
y=-z
z=-y
puis que vous noter:

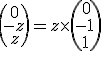
vous mettez 'z' mais on aurait pu mettre n'importe quelle lettre? ce que vous montrez c'est que le y entraine le z et inversement?

2ème point: Donner 2 vecteurs colinéaires de A.
En fait il faut donner un vecteur avec seulement 2 valeurs distinctes car la dimension est 2?
D'où les deux '0' dans le premier exemple et les deux '-1' dans le second?

Voilà les points qui ne sont pas très clairs le reste a été compris.
Merci à vous.

Premier point,

Tu tournes en rond !

Il faut exprimer x,y,z en fonction d'une seule variable réelle .
J'ai choisi z
ainsi :
x=0
y=-z
z=z

J'aurais pu choisir un réel k quelconque , ce qui aurait donné :
x=0
y=-k
z=k

Même conclusion bien sûr

Second point

J'explicite le raisonnement.

La dimension étant 2, toute base de Imf est constituée de deux vecteurs du type (x,y,z) de $R^3$ non colinéaires.
Il faut donc que tu trouves deux vecteurs -images , non colinéaires, de $R^3$

Il faut que tu aies à l'esprit ce que représente la matrice A de f

Le vecteur-première colonne de A est l'image du premier vecteur de la base canonique de $R^3$ (c'est à dire (1,0,1)
Le vecteur-seconde colonne de A est l'image du second vecteur de la base canonique de $R^3$ (c'est à dire (0,1,0)
Le vecteur-troisième colonne de A est l'image du troisième vecteur de la base canonique de $R^3$ (c'est à dire (0,0,1)

Ces 3 vecteurs-colonnes de la matrice A sont donc des vecteurs-images .
Ils sont dans Imf
Il suffit donc d'en choisir deux non colinéaires.

Bonnes réflexions.

Je sais que des vecteurs colinéaires vont dans la même direction. Je sais le démontrer pour deux vecteurs(https://www.kartable.fr/ressources/mathematiques/methode/montrer-que-deux-vecteurs-sont-colineaires/3623) par contre pour 3 vecteurs je ne sais pas le démontrer.

je pensais néanmoins à ça comme valeurs de vecteurs (0,1,0) et (1,0,1) ou (0,1,0)et(1,1,0)

Ce ne sont pas trois vecteurs non colinéaires que tu cherches mais DEUX

Tu choisis donc DEUX vecteurs-colonnes non colinéaires de la matrice.

C'est une "évidence" que (-2,2,0) et (0,-1,-1) ne sont pas colinéaires !
Si tu veux le justifier par un calcul très simple, tu cherches un réel k tel que
(-2,2,0) =k (0,-1,-1)
tu obtiens le système
$- 2 = k (0)$
$2 = k (- 1)$
$0 = k (- 1)$
Je te laisse trouver que système est impossible
k n'existe pas
les deux vecteurs choisis ne sont pas colinéaires.

effectivement je n'ai trouvé aucune valeur de k permettant de trouver -2, 2 et 0, c'est pour cela que ce n'est pas colinéaire

oui !

(Je pense que tu veux dire que les deux vecteurs choisis ne sont pas colinéaires)

Oui c'est ce que je voulais dire

D'accord.

Approfondis tout cela.

Merci de m'avoir expliqué ce point

Bonjour Dut,

Quelques indications pour ta seconde question relative au polynôme minimal.

Le polynôme minimal est diviseur du polynôme caractéristique
Le polynôme minimal a les mêmes racines que le polynôme caractéristique
Le polynôme minimal est unitaire ( le coefficient de son terme de plus fort degré est 1)

Un exemple,

Soit la matrice
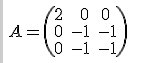
Tu cherches le polynôme caractéristique que j'appelle Pcar
Tu dois trouver, après calculs
$Pcar(x)=(2-x)[(-1-x)^2-(-1)^2]=(2-x)(x^2+2x)$

En factorisant :
$P c a r (x) = (2 - x) (x) (x + 2) = - (x - 2) (x - 0) (x + 2)$

Les valeurs propres (distinctes) de A sont 0,2,-2.

Avec la définition donnée, tu dois déduire que le polynôme minimal, que j'appelle Pmin, est :
$Pmin(x)=x(x-2)(x+2)\fbox{Pmin(x)=x(x-2)(x+2)}$

Remarque : ce cas est le plus simple.
C'est un peu plus compliqué lorsque le polynôme caractéristique n'a pas toutes ses racines distinctes.

Bonjour Mtschoon,
J'arrive à vous suivre et obtenir les mêmes résultats jusqu'au polynome minimal.
Après ça se complique, je n'ai peut être pas bien compris les définitions.
racine et valeurs propres veulent dire la même chose?
Dans Pmin(x) '0'(valeur propre) disparait c'est que 0 n'est pas diviseur?
Enfin je ne comprends pas pourquoi le x est sorti

PS: vous noter (2-x) mais ça ne serait pas (-2-x)?

J'essaie de répondre à tes questions.

Les "racines" ou "zéros" sont les valeurs qui annulent un polynôme (ou une fonction de façon générale).
Elles sont les "valeurs propres", lorsqu'il s'agit du polynôme caractéristique Pcar.

Pour Pmin(x), la valeur 0 ne disparait pas !
x=(x-0) (mais (x-0) est une écriture un peu enfantine...)
Tu peux écrire :
$Pmin(x)=(x-0)(x-2)(x+2)\fbox{Pmin(x)=(x-0)(x-2)(x+2)}$

A tes deux dernières questions :
" je ne comprends pas pourquoi le x est sorti" ???
Détaille mieux en indiquant où est ton problème.
"vous noter (2-x) mais ça ne serait pas (-2-x)"???
Détaille mieux en indiquant où tu mets (-2-x) au lieu de (2-x)

$Pmin(x)=x(x-2)(x+2)\fbox{Pmin(x)=x(x-2)(x+2)}$
Voilà le x sorti que je ne comprends pas.

$Pcar(x)=(2-x)[(-1-x)^2-(-1)^2]=(2-x)(x^2+2x)$
$P c a r (x) = (2 - x) (x) (x + 2) = - (x - 2) (x - 0) (x + 2)$

Bien vu pour la matrice !
Les calculs sont faits avec la matrice
2....
......

Par contre pour la "sortie" de x, je ne vois pas trop ton problème.
C'est peut-être la factorisation de $x^2+2x$ qui te gène .

$x^2+2x=x(x+2)$

Pour compléter ces notions de polynôme minimal , je t'indique des réponses pour la matrice que tu as indiqué dans ton énoncé, c'est à dire

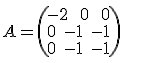
Tu auras ainsi les deux cas usuels pour trouver le polynôme minimal.

Après calculs, tu dois obtenir:
$Pcar(x)=(x^2+2x)(-2-x)=x(x+2)(-2-x)$
$P c a r (x) = (x - 0) (x + 2) (- 2 - x) = - (x - 0) (x + 2) (x + 2)$

Pour trouver le polynôme minimal satisfaisant aux 3 conditions que je t'ai indiqué, tu as ici un choix à faire :
$(x - 0) (x + 2)$ ou bien $x-0)(x+2)^2$

Tu commence par regarde le plus simple, c'est à dire $(x - 0) (x + 2)$

Pour savoir s'il convient , tu dois calculer $(A - 0 I) (A + 2 I)$
Si tu obtiens la matrice nulle (composée de 9 zéros), c'est bon : c'est le polynôme minimal.
Sinon, c'est l'autre.

Ici, sauf erreur , Pmin(x)=x(x+2)

Remarque : avec le polynôme minimal (sans passer par les vecteurs directeurs), on peut savoir si une matrice est diagonalisable, mais j'ignore si cela fait partie de ton cours.

Bonnes révisions.

Bonjour Mtschoon,
Merci pour l'explication.
Pour l'instant je n'ai juste un problème avec le calcul de polynome.
Je n'arrive pas au même résultat que vous, je vous mets mon calcul.
-2-x.((-1-x)² -1)
-2-x.(1+2x+x²-1)
-x^3 -2x² -2

Après vérification de la méthode j'obtiens:
(-2-x)(x²+2x)
-x^3-4x²-4x

Ton dernier calcul est juste, mais tu fais la même chose que dans un précédent topic : tu développes tout et tu te retrouves avec un polynôme du troisième degré qu'il faut factoriser (et que tu ne sais guère factoriser...) !

Comme indiqué dans ce précédent topic, c'est beaucoup plus facile de factoriser AVANT.

$Pcar(x)=(-2-x)(x^2+2x)$

Tu gardes $(- 2 - x)$

Tu factorises ( $x^2+2x$ ) :

$x^2+2x)=x(x+2)=(x-0)(x+2)$

Conclusion :

$Pcar(x)=(-2-x)(x-0)(x+2)=-(x+2)(x-0)(x+2)=-(x-0)(x+2)^2$

C'est bon pour la factorisation j'ai bien trouver le bon résultat.
Par contre pour le polynome pourquoi on a le choix entre (x−0)(x+2) et (x−0)(x+2)² ?
Pour voir si la matrice est nulle je comprends bien comment faire par contre pour le calcul (A−0I)(A+2I) où faut-il utiliser (x−0)(x+2) ?

Le choix vient du fait que les deux polynômes indiqués conviennent aux 3 critères satisfaisant le polynôme minimal.

Pour ta seconde question : c'est du cours...
(x−0)(x+2) est associé à (A-0I)(A+2I)
(x−0)(x+2)² est associé à (A-0I)(A+2I)²

Merci Mtschoon je n'avais pas compris pour la seconde question mais maintenant c'est bon je même retrouvé la matrice nulle en faisant le calcul.
Merci pour tout.

De rien Dut,

Quelque chose, dans tes questions, me laisse perplexe...

Tout tourne autour des matrices diagonalisables ou non diagonalisables : polynôme caractéristique, valeurs propres, vecteurs propres, polynôme minimal (qui permet de savoir directement si la matrice est diagonalisable) mais tu ne poses pas de questions sur la recherche, lorsqu'elle existe, de la matrice diagonale D.
C'est pourtant très important car elle permet de simplifier les calculs relatifs à la matrice (les puissances notamment)

Alors, si cela fait partie de ton programme de révision (que j'ignore), n'oublie pas de revoir cette notion.

Bonnes révisions.

J'avais compris que les matrices diagonales étaient juste une matrice avec les valeurs propres dans la diagonale les autres coefficients étant à 0.

Par exemple une des questions présente est donner une matrice diagonale et une matrice inversible Pj telles que M= Pj Dj Pj ^-1
J'utilise la méthode 1 montrée ici:
https://fr.wikihow.com/calculer-l'inverse-d'une-matrice-3x3

C'est tout-à-fait ça .

Toute matrice diagonale D est très simple (composée avec les valeurs propres) et ses puissances aussi.

$D^k$ est la matrice diagonale dont la diagonale est composée des valeurs propres à la puissance k.

Vu que $M=PDP^{-1}$ , elle permet de simplifier les calculs sur les puissances de la matrice M avec $M^k=PD^kP^{-1}$

Si tu le souhaites, tu peut consulter l'exercice 1 (avec la correction) du lien ci-dessous

http://exo7.emath.fr/ficpdf/fic00054.pdf

Bon courage pour la suite.

Merci pour tout Mtschoon.
Bonne semaine