Equation du second degré dans C, à coefficients complexes

Bonjour,
Je dois résoudre des équations avec des complexes. Je ne sais pas faire, j'en ai surement déjà fait mais je ne suis même pas sur. Ce qui me gène est la partie réelle/imaginaire.
Par exemple pour: iz²+(1-5i)z+6i-2=0
je ne sais pas comment traiter le iz²
en l'ignorant après avoir cherché sur internet je trouve:
z=(-6i+2)/(1-5i)
z=(6i+30-2-10i)/(-1+25)
z=(4i)/24 + 28/24
= 1/6i +7/6
Voila le résultat qui est faux je le sais car je n'ai pas pris en compte le iz² ne sachant pas comment le traiter, merci.

Bonjour Dut,

Tu as à résoudre une équation du second degré d'inconnue z complexe, à coefficients complexes, de la forme $az^2+bz+c=0$

$a = i$
$b = 1 - 5 i$
$c = 6 i - 2$

Pour les formules, regarde ici :
http://lescop.gmp.free.fr/IMG/pdf/trinome_complexe.pdf

Je viens de faire les calculs.
Si tu comprends la méthode, je t'indique ce que tu dois trouver :

Discriminant $Δ=−2i\Delta=-2i$

Racines carrées complexes de $Δ\Delta$ : 1-i et -1+i
Tu prends pour $δ\delta$ une des deux ( cela revient au même)
Par exemple $δ=1−i\delta=1-i$

Solutions de l'équation du second degré proposée :
$x_1=2$
$x_2=3+i$

Bons calculs !

Une remarque : les années passées, dans les exercices que tu proposais, tu utilisais la notation j avec $j^2=-1$
Cette fois, c'est la notation i qui est utilisée.
C'est la notation la plus usuelle en mathématiques, donc ici $i^2=-1$

Si tu veux éventuellement les détails des calculs de la résolution, indique-le.

Bonsoir Mtschoon,
Merci pour votre réponse rapide.
Effectivement les notations ont changées car le professeur qui dispensait les cours jusqu'à présent a pris sa retraite.
Je n'ai pas le même résultat, je veux bien, si possible de détail pour au moins x1 je me débrouillerai pour x2.
Merci beaucoup.

Bonsoir Dut,

As-tu déterminé $Δ\Delta$ et $δ\delta$ ?

Si ce n'est pas le cas, demande les détails.

Si c'est le cas :

$x1=−b+δ2=−1+5i+1−i2i=4i2i=2(2i)2i=2x_1=\frac{-b+\delta}{2}=\frac{-1+5i+1-i}{2i}=\frac{4i}{2i}=\frac{2(2i)}{2i}=\fbox{2}$

$x2=−b−δ2=−1+5i−1+i2i=−2+6i2ix_2=\frac{-b-\delta}{2}=\frac{-1+5i-1+i}{2i}=\frac{-2+6i}{2i}$

Tu sais que $1=i^2$ donc $2=2i^2$

donc: $x2=2i2+6i2i=2i(i+3)2i=i+3=3+ix_2=\frac{2i^2+6i}{2i}=\frac{2i(i+3)}{2i}=i+3=\fbox{3+i}$

Remarque : pour mettre $x_2$ sous forme algébrique, à partir de $−2+6i2i\frac{-2+6i}{2i}$ , tu peux aussi multiplier le numérateur et le dénominateur par le conjugué de $2 i$ c'est à dire $- 2 i$ et tu trouveras, après simplifications, le même résultat $3 + i$
C'est la méthode classique lorsqu'il n'y a pas plus simple.

Tu peux aussi de contenter de multiplier le numérateur et le dénominateur par $i$ ou $- i$ et tu trouveras, après simplifications, le même résultat $3 + i$

Pour t'entraîner, pour $x_2$ , tu peux faire les 3 démarches.

Bons calculs.

Bonjour Mtschoon,
J'ai bien déterminé DELTA mais pour la lettre grecque (qui se dit aussi delta si je me trompe pas) je n'arrive pas à déterminer le résultat.
cela devrait etre égal à $i−Δi\sqrt{-\Delta}$ je ne sais pas faire le calcul principalement à cause du i
puis dans x1 et x2 le numérateur est 2i vous ne mettez que 2 je pense donc que vous avez réalisée une simplification avec $δ\delta$ (delta triangle)

Pour $δ\delta$ , je me doutais un peu que tu ne connaissais pas trop...
(Effectivement $δ\delta$ qui se lit" delta minuscule" ou "petit delta")

$i−Δi\sqrt{-\Delta}$ a un sens si et seulement si $Δ\Delta$ est un réel négatif donc si $−Δ-\Delta$ est un réel positif
Ici, $Δ\Delta$ est complexe non réel.

Ici, tu dois trouver les racines carrées complexes de $Δ\Delta$ c'est à dire les nombres complexes (de la forme $a + b i$ avec a et b réels) donc le carré vaut $Δ\Delta$ (que l'on pourra appeler $δ\delta$ et $−δ-\delta$ )

$\fbox{(a+bi)^2=-2i}$

Tu développes le carré (identité remarquable usuelle)
$a^2+2abi+i^2b^2=-2i$

vu que $i^2=-1$ , tu obtiens
$a^2+2abi-b^2=0-2i$

Dans cette égalité, tu identifies les parties réelles entre elles et les parties imaginaires entre elles:
$a^2-b^2=0$ (formule 1)
$2 a b = - 2$ <=> $a b = - 1$ (formule 2)

Tu dois résoudre ce système
(désolée, il manque les accolades qui actuellement ne sont pas prévues sur cette version de Latex)

formule 2 <=> $b=−1ab=-\frac{1}{a}$

Tu substitues dans la formule 1:
$a2−1a2=0a^2-\frac{1}{a^2}=0$ <=> $a2=1a2a^2=\frac{1}{a^2}$ <=> $a^4=1$ <=> $a^2=1$

$a^2=1$ <=> $a=1\fbox{a=1}$ ou $a=-1\fbox{a=-1}$
Pour $a = 1$ , la formule 2 permet d'obtenir $b=-1\fbox{b=-1}$
Pour $a = - 1$ , la formule 2 permet d'obtenir $b=1\fbox{b=1}$

Les deux racines carrées complexes de $- 2$ i sont donc $1 - i$ et $- 1 + i$

Tu appelles $δ\delta$ une des deux (au choix) ; l'autre sera forcément $−δ-\delta$

Pour les calculs de $x_1$ et $x_2$ , j'ai pris $\fbox{\delta=1-i}$

Regarde cela de près.

Remarque : pour résoudre le système ( pour trouver les racines carrées complexes de $Δ\Delta$ ) on peut associer l'égalité des modules lorsque c'est difficile.
Je ne l'ai pas fait car c'était simple et javais peur de te compliquer .

Pour répondre à ta question sur $x_1$ et $x_2$ :
Pour $x_1$ et $x_2$ , le numérateur et le dénominateur se simplifient par 2i.
Si ce n'est pas cela dont tu parles, précise.

Bons calculs.

@mtschoon a dit dans Equation du second degré dans C, à coefficients complexes :

Pour $δ\delta$ , je me doutais un peu que tu ne connaissais pas trop...
(Effectivement $δ\delta$ qui se lit" delta minuscule" ou "petit delta")

$i−Δi\sqrt{-\Delta}$ a un sens si et seulement si $Δ\Delta$ est un réel négatif donc si $−Δ-\Delta$ est un réel positif
Ici, $Δ\Delta$ est complexe non réel.

Ici, tu dois trouver les racines carrées complexes de $Δ\Delta$ c'est à dire les nombres complexes (de la forme $a + b i$ avec a et b réels) donc le carré vaut $Δ\Delta$ (que l'on pourra appeler $δ\delta$ et $−δ-\delta$ )

$\fbox{(a+bi)^2=-2i}$

Tu développes le carré (identité remarquable usuelle)
$a^2+2abi+i^2b^2=-2i$

vu que $i^2=-1$ , tu obtiens
$a^2+2abi-b^2=0-2i$

Dans cette égalité, tu identifies les parties réelles entre elles et les parties imaginaires entre elles:
$a^2-b^2=0$ (formule 1)
$2 a b = - 2$ <=> $a b = - 1$ (formule 2)

Bonjour Mtschoon, je suis désolé pour le délai de réponse.
La première partie est comprise, merci. Je bloque néanmoins à partir "d'identifier la partie imaginaire et réelle" pour moi la partie imaginaire est représentée par i.

Bonjour Dut,

Je t'indique le Principe :

Sous forme algébrique, tout nombre complexe z s'écrit sous la forme z=a+bi , a et b étant réels.
a s'appelle la partie réelle de z
b s'appelle la partie imaginaire de z

Soit deux nombres complexes z et z' mis sous forme algébrique
$z = a + b i$
$z^{'} = a^{'} + b^{'} i$

z=z' équivaut à :

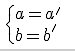
C'est ce qu'on appelle "identifier les parties réelles entre elles, et les parties imaginaires entre-elles.

Merci beaucoup pour l'explication Mtschoon, j'ai compris.

Parfait !
Bon travail, Dut.