Relation d'ordre / itérée

Bonjour, comme je vous le disais il y a quelques jours j'ai des problèmes sur les relations.
J'ai sélectionné un exercice que j'ai pu faire en partie.

On note C={0,1,2....,9}, l'ensemble des chiffres en base 10. On considère l'écriture de ces chiffres dans un afficheur à diodes électro-luminescentes(LED) comme ceci:

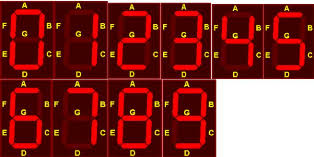
On définit une relation binaire R sur C en posant c1 R c2 si et seulement si c1 est "inclus" dans c2, au sens où tout segment allumé pour afficher c1 est aussi allumé pour afficher c2.

J'ai pu dessiner le graphe de la relation R.

Après il faut montrer que c'est une relation d'ordre sur l'ensemble {0...9} et dire c'est un ordre total;

j'ai bien vu quelle est réfléxive et transitive par contre j'ai un doute pour l'antisymetrie.

Prenons par exemple c1= 1 et c2=7 c1 est bien inclus dans c2 mais c2 n'est pas inclus dans c1
Alors que pour que se soit antisym il faut avoir C1 R C2 et C2 R C1 que c1 soit inclus dans c2 et inversement c2 inclus dans c1.

Enfin dernière question: quand il est demandé la matrice associée à la relation itérée R2
--> je prends la matrice R et je fais le produit R*R pour obtenir r²?

Merci beaucoup

Bonjour Dut,

Pour ta question sur la relation d'ordre :
il faut que tu revois la définition d'antisymétrie...( tu confonds avec la symétrie)

Pour ta seconde question :
la composition de relations correspond au produit de matrices.
La relation réitérée veut dire R o R , notée R²
En appelant M la matrice de R, tu dois donc faire M xM c'est à dire M².
Ta seconde idée est bonne.

Rebonr Dut,

J'espère que tu as eu le temps de revoir la définition d'antisymétrie :
$C_1 R C_2$ et $C_2 R C_1$ => $C_1=C_2$
Tu peux vérifier que cette propriété est vraie

R est donc réflexive, antisymétrique et transitive c'est une relation d'ordre.

L'ordre n'est pas total
Par exemple : 1 R 2 est faux et 2 R 1 est faux

Bon travail.

Bonsoir Mtschoon,
tout en ayant les définitions à côté de moi, je n'arrive pas à dissocier la symétrie de l'antisymétrie. Prenons 1 R 5 et 5 R 1, dans ce cas 1 n'est pas égal à 5? vu que j'ai donné un peu plus haut (par confusion) la définition de la symétrie on voit bien avec les exemples que 1 n'est pas inclus dans 5 donc la relation n'est pas symétrique, j'espère ne pas dire de bêtises. Mais dans le cas de l'antisymétrie c1=c2 ce = représente bien l'inclusion aussi qui est dans la consigne pour expliquer la relation?

La symétrie traduit le fait que $C_1 R C_2$ => $C_2 R C_1$
Ici, la relation R n'est pas symétrique
Par exemple : $1 R 4$ est vraie alors que $4 R 1$ est fausse

Pour l'antisymétrie, tu cherches dans quels cas , $C_1 R C_2$ et $C_2 R C_1$ sont TOUS les DEUX vraies.
Si tu trouves que cela ne se produit que lorsque $C_1=C_2$ , tu peux déduire que la relation R est antisymétrique.
Ici, la relation R est antisymétrique

Bonjour Mtschoon, je crois que ce qui me perturbe est le = de l'antisymetrie. J'ai fait un schéma simplifié ou on enlève la réflexivité etc afin d'avoir un schéma plus lisible

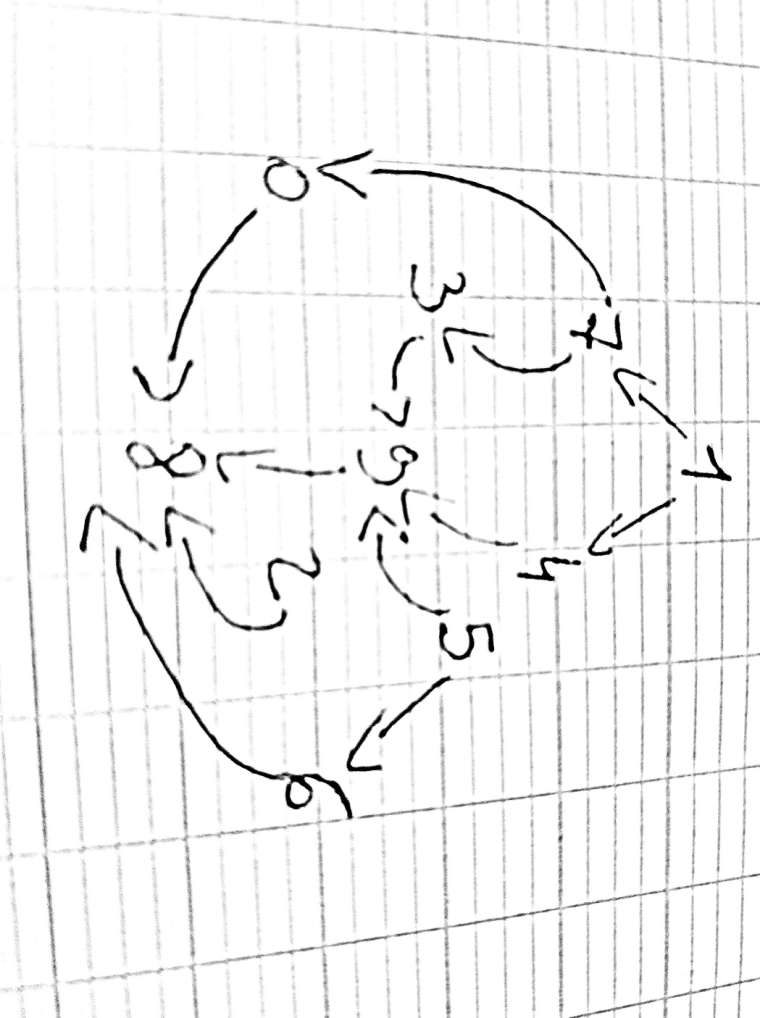
Pour moi si on dit C1=C2 cela signifie que c'est le même chiffre.

Tout à fait !

C1=C2 veut dire que C1 et C2 sont "le même chiffre".

Ici, c'est seulement lorsque C1 et C2 sont "le même chiffre" que l'on peut avoir vraies en même temps C1 R C2 et C2 R C1

Si C1 et C2 ne sont pas "le même chiffre" on a jamais à la fois C1 R C2 et C2 R C1 vraies en même temps.

D'accord c'est plus clair. Merci beaucoup

Pour (peut-être) t'éclairer sur l'antisymétrie , je te mets un lien qui me semble intéressant :
http://gilles.dubois10.free.fr/Bases/Relations/antisymetrie.html
Bonne réflexion.