Relation d'équivalence

Bonjour, pourriez-vous m'aider sur la compréhension de l'énoncé suivant:
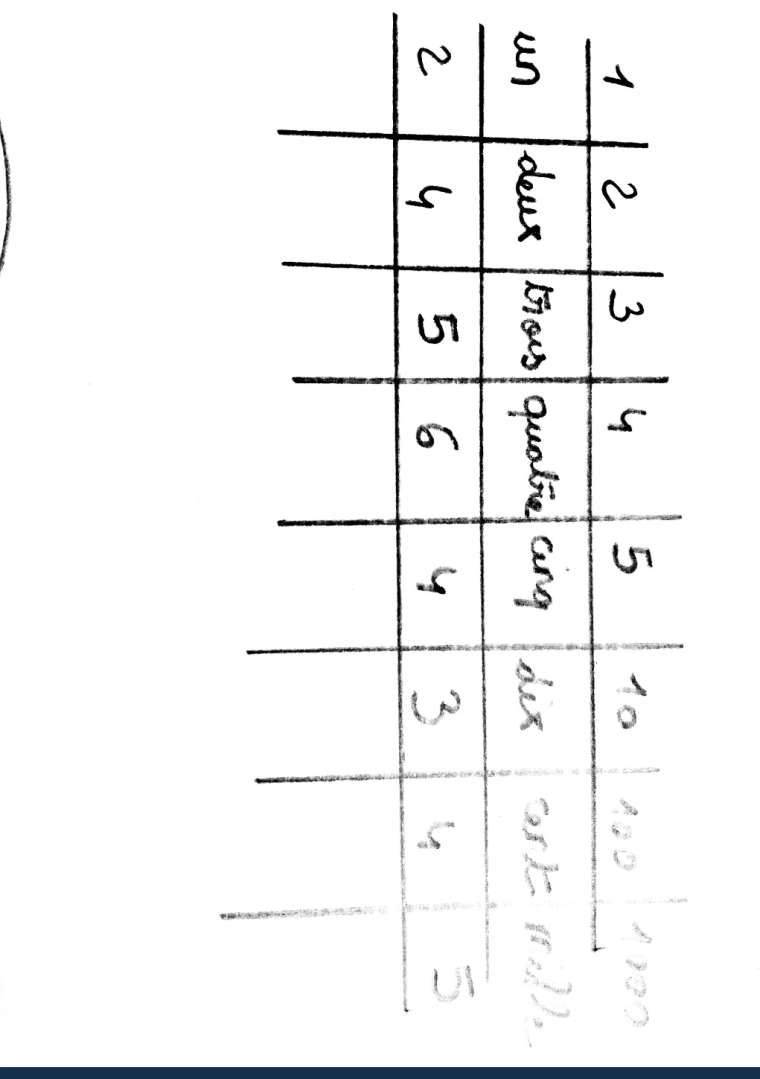
Soit X l'ensemble de nombres: X={1,2,3,4,5,10,100,1000}. On définit la fonction f: X-->N par:
f(x) = le nombre de lettres dans l'écriture de x en français

a) remplir un tableau de 3 lignes comme suit:
1ére ligne: x élément de X
2ème: l'écriture de x en français
3ème: la valeur de f(x)

Voir Photo ci-après

b) Quelle est la partition de X fournie par les images réciproques de f?

c) Décrire la relation d'équivalence R sur X correspondant à cette partition de X. d'une part en dessinant son graphe et d'autre part en donnant tous ses élément (rappel R est un sous ensemble de X²)

Donc il faut que sa soit refléxive transitive et symétrique. je voulais faire les relations entre la 1ère ligne du tableau et la dernière mais pour quatre on a 6 lettres et le 6 n'est pas présent

d) Dans cette relation d'équivalence, quelle est la classe de 1000?

Dut bonjour,

a)Oui pour ton tableau

b) X={1,2,3,4,5,10,100,1000}

En appelant f(X) l'ensemble des images par f des valeurs de X, on obtient, grâce au tableau : f(X)={2,3,4,5,6}

On cherche les antécédents (images réciproques) , par f, des valeurs de f(X)
L'ensemble des antécédents de 2 est {1}
L'ensemble des antécédents de 3 est {10}
L'ensemble des antécédents de 4 est {2,5,100}
L'ensemble des antécédents de 5 est {3,1000}
L'ensemble des antécédents de 6 est {4}

{[1},{10},{2,5,100}, {3,1000},{4}} constitue une partition de X

(Une partition est un ensemble de parties disjointes de X dont la réunion est X)

c) La relation R, sur X, correspond à cette partition, peut s'écrire :
"a même nombre de lettres , dans l'écriture française, que "

Exemples pour comprendre :
2 R 5 est vraie car 2 et 5 ont même nombre de lettres dans l'écriture en français
2 R 6 est fausse car 2 et 6 n'ont pas le même nombre de lettres dans l'écriture en français

Je pense que tu pourras aisément faire le graphe de cette relation R

Pour prouver que R est une relation d'équivalence, tu prouves (de façon générale) les 3 propriétés usuelles

x a même nombre de lettres dans l'écriture en français que x
donc x R x est vraie (réflexivité)

Si x a même nombre de lettres dans l'écriture en français que x' (c'est à dire que x R x' est vraie), forcément x' a même nombre de lettres dans l'écriture en français que x (c'est à dire que x' R x est vraie (symétrie)

Si x a même nombre de lettres dans l'écriture en français que x' (c'est à dire que x R x' est vraie), et si x' a même nombre de lettres dans l'écriture en français que x" (c'est à dire que x' R x" est vraie), forcément x a même nombre de lettres dans l'écriture en français que x" (c'est à dire que x R x" est vraie) (transitivité)

d) Vu que R est une relation d'équivalence sur X, les parties {1},{10},{2,5,100}, {3,1000},{4} qui constituent la partition de X s'appellent des classes d'équivalence.
Tout élément de chacune de ces parties s'appelle un représentant de la classe.
Tous les éléments d'une même classe sont liés par la relation d'équivalence.

La classe de 1000 est donc la partie {3,1000}
(1000 est un représentant de cette classe)

Si on t'avait demandé la classe de 2, tu aurait dû répondre :
la classe de 2 est la partie {2,5,100}
(2 est un représentant de cette classe)

Si on t'avait demandé la classe de 5, tu aurait dû répondre :
la classe de 5 est la partie {2,5,100}
(5 est aussi un représentant de cette classe)

J'ai fait au mieux.
Reposte si besoin.

Bonjour Mtschoon,
merci pour cette rédaction très claire. J'ai bien compris

C'est très bien Dut,
Vu que tu as bien compris, cela valait la peine d'expliquer au mieux.