Relation binaire/relation de préordre
-
Ddut dernière édition par
Bonjour j'ai refait un exercice présent sur les annales. Avez-vous la possibilités de me dire si mon raisonnement est juste?
Sur l’ensemble X={a,b,c,d,e,f}, on considère la relation binaire R={(a,b),(a,d),(b,e),(c,f),d,c),(e,f)}
a. Dessiner le graphe R
b. Quelle est la matrice de la relation R?
c. Quelle est la matrice de la relation R²
d. Quelle est la relation de préordre engendrée par R? (Vous pouvez utiliser les graphes ou les matrices, au choix, pour justifier votre réponse)
-
Ddut dernière édition par
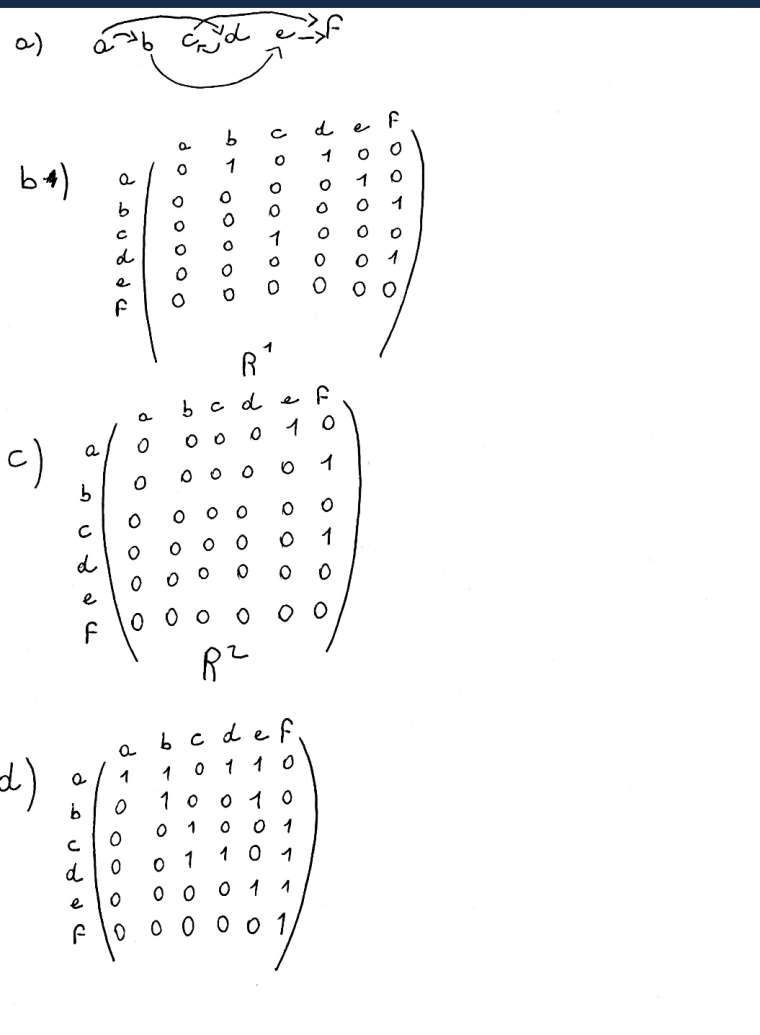
-
mtschoon dernière édition par

Dut bonjour,
Je regarde
a) c'est bon
b) c'est bon
c) Je crois voir une erreur à la première ligne.
Sauf erreur la première ligne de la matrice de R² devrait être :
0 0 1 0 1 0
Vérified) Pour satisfaire la réflexivité, c'est bon : tu as bien mis des 1 sur toute la diagonale principale.
Pour satisfaire la transitivité, je crois voir deux manques
a R d et d R c => a R c : il faut mettre un 1 à (a,c)
b R e et e R f => b R f : il faut mettre un 1 à (b,f))
Vérifie.
-
Ddut dernière édition par
Bonjour Mtschoon, effectivement ce sont des erreurs de ma part. je pense vraiment avoir bien compris maintenant, j'essaie juste de gagner en rapidité en refaisant des annales et en faisant le moins d'erreurs possible (ce qui est encore difficile, la preuve) car le temps me manque en examen.
A titre de curiosité à quoi sert R² car il y a beaucoup de 0? et si on continue avec R^3 r^.... on bout d'un moment on se retrouve sans doute avec une matrice =0
-
mtschoon dernière édition par mtschoon

R2R^2R2 est la relation composée de RRR avec RRR, c'est à dire "RRR suivie de RRR" , notée RoR=R2RoR=R^2RoR=R2
Dans ton exercice, le calcul de la matrice de R2R^2R2 sert visiblement à savoir si l'étudiant sait faire le calcul, car aucune question suivante l'utilise.
Tu as tout à fait raison : MnM^nMn est la matrice nulle pour n≥4n\ge 4n≥4
Bon travail.
-
Ddut dernière édition par
Merci beaucoup Mtschoon.
A bientôtPS: je vous ai envoyé un MP
-
mtschoon dernière édition par

Contente que tes épreuves se soient bien passées.
Je viens de répondre à ton MP, mais ce n'est pas très commode.
Si tu as besoin, pour plus de clarté, ouvre une discussion pour poser ta question.Bon week-end.
-
mtschoon dernière édition par mtschoon

Félicitations Dut pour ta belle note en "Maths discrètes"
que tu viens de m'indiquer par MP. Le travail paye !