Etienne et son enclos rectangulaire

Bonjour j'aurais besoin d'aide s'il vous plait
VOIS CI MON SUJET .

Etienne souhaite construire un enclos rectangulaire pour ses chiens.
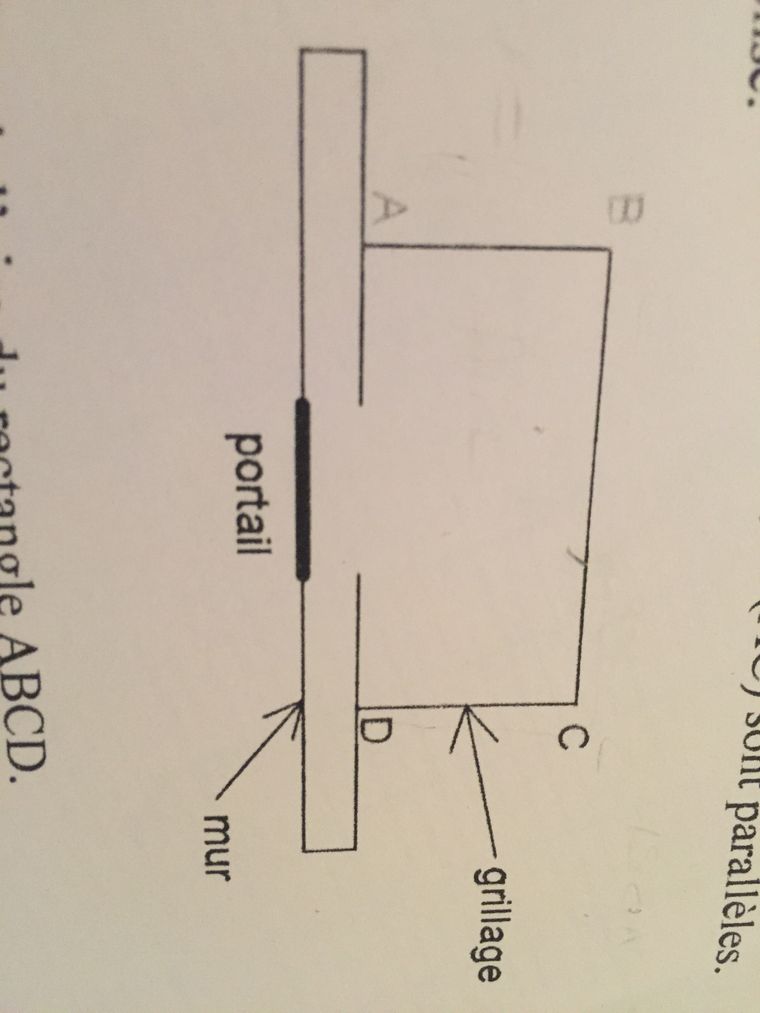
Il possede 15m de grillage a disposer de la facon suivante:

PARTIE 1

Entre quelles valeurs x est-il compris?
Exprimer en fonction de x les lonsgueurs CD, BC, puis l'aire du rectangle ABCD?

maeva, bonjour,

Ton énoncé ne semble pas complet

Tu as écrit " de la façon suivante" mais tu n'indique pas la façon...
Qui est x ?

@mtschoon AB=x

@mtschoon la facon suivante est l'image que je n'avais pas poster excuser moi.

@maeva

Merci pour ces précisions.

Quelque chose me dérange dans cet énoncé ; c'est le portail.
As-tu des éléments le concernant ?

Pistes, en admettant que le portail n'est pas grillage (c'est le plus simple vu que l'on a pas sa dimension...)

AB=x . Nécessairement $0≤x≤150\le x\le 15$

CD=AB=x

Soit BC=y

Le périmètre du grillage est AB+BC+CD=2x+y
$2 x + y = 15$ <=> $y = 15 - 2 x$

Aire du rectangle : $AB \times BC = x\times y$

En appelant f(x) l'aire du rectangle en fonction de x :

$f(x)=x×(15−2x)f(x)=x\times (15-2x)$

Tu peux transformer cette expression.

Bonne suite pour cet exercice.

@mtschoon Non le portail ne fait pas partis du grillage sachant qu'il y a le mur donc je suppose que le grillage fais partie du rectangle ABCD et on plus.

Merci pour votre aide mais je ne comprends pas bien X=? quelle dimension?

et j'ai une autre partie 3
qui est: Comme Etienne pense au confort de ses chiens , il souhaite finalement construire un enclos dont l'aire serait la plus grande possible avec 15m de grillage. Quelles semblent etre les dimensions de cet enclos?

D'accord.

On considère que le grillage est donc composé des parties AB, BC, CD.

Je viens de donner mes pistes ainsi.

x=AB
Sans avoir fait aucun calcul, tu peux seulement dire que la valeur x est forcément inférieure la longueur de 15 m de grillage
Vu qu'une longueur est un réel positif, x est compris entre 0 et 15
Pour la 3ème partie, il faut que tu étudies les variation de la fonction f, pour x compris entre 0 et 15.
Tu pourras en déduire la valeur de x (puis y) pour que l'aire du rectangle soit maximale.

@mtschoon d'accord merci beaucoup pour votre aide j'ai enfin compris car j'etais perdu. Merci beaucoup encore. Bonne journee a vous.

@maeva

De rien !
Reposte si tu as besoin d'une vérification pour ta réponse à la question 3.