multiple d'un polynôme (Réseaux-Code CRC)

Bonjour,
j'ai deux polynômes:
c(x)=1000=x3
g(x)=x⁴+x²+x+1
On me demande si de vérifiez que C(x) est un multiple de G(x) mais je ne sais pas vraiment faire avec des polynômes.

Merci pour votre aide.

Dut bonjour,

$C (x$ ) multiple de $G (x)$ veut dire qu'il existe un polynôme $Q (x$ ) tel que $\fbox{C(x)=G(x)\times Q(x)}$

Je te mets un lien
http://homeomath2.imingo.net/polymult.htm

Tu as dû faire une faute de frappe sur $C (x$ ) car tu as écrit
"c(x)=1000=x3 ???

Merci de re-écrire C(x)

Merci Mtschoon pour votre réponse.
Pour c(x) j'ai trouvé en binaire le résultat 1000 ce qui, si j'ai bien compris correspond au polynome: 0+0x+0x²+x³ d'où le x³
Comment puis-je trouver Q(x) est-ce des calculs à appliquer ou est-ce de la logique?

Merci

Si j'ai bien compris,

$G(x)=x^4+x^2+x+1$
G est un polynôme de degré 4

En multipliant G(x) par un polynôme Q(x) on obtient un polynôme de degré au moins égal à 4 (somme de degré de G avec le degré de Q)

$C(x)=x^3$
C est un polynôme de degré 3

L’égalité entre polynômes C(x)=Q(x)G(x) ne peut donc pas être vraie.

Le C(x) que tu indiques ne peut pas être multiple de G(x) au sens mathématique des polynômes.

Je ne suis pas sûre que l'on parle de la même chose...

c'est un exercice sur les codes CRC.
On est d'accord pour G(x) après pour c(x) j'ai fais une divison en binaire et je trouve 1000 je pensais que 1000=x³ mais ce n'est peut être pas ça.
Voila les questions en rapport:
D(x) est la représentation polynomiale du message 10011101
On veut ”protéger”D(x) avec le polynome générateurG(x) =x4+x2+x+ 1. Combien de bits va-t-on ajouter ? 4 bits car d°4

Quels sont les bits à ajouter pour former le mot codé C(x) à transmettre (donner votre calcul manuel) ? j'ai trouvé 1000 (Résultat vérifié avec un camarade)

Vérifiez queC(x) est un multiple deG(x) (donner votre calcul manuel) --> Question qui pose problème.

Je pensais que c'était un problème mathématique mais ce n'est peut être pas le cas

Si ça peut t'être utile, je te mets un lien vers un document relatif au code CRC qui n'est vraiment pas mon domaine...
Il semble s'agir de "code détecteur d'erreurs dans les réseaux de transmission"...on est loin des maths générales...
http://www.iro.umontreal.ca/~mignotte/IFT1215/ExosSupplementaires/ADuvallet.pdf
(il y a plusieurs pages à consulter sur le CRC)

$1000=x^3$ est cohérent, mais je ne peux pas t'en dire plus, sauf peut-être vérifier si le '1000' dont tu parles est exact, et SURTOUT regarder ton cours, pour comprendre ce qu'est véritablement le "mot codé" C(x).
C(x) n'est peut-être pas ce que tu penses...

*Tu écris "bits à ajouter pour former le mot codé C(x)"
Essaie de savoir à qui et comment il faut les ajouter ces bits.
Je pense que c'est à D(x) , mis en binaire, qu'on les ajoute.

Les bits à ajouter ne représentent pas le mot codé C(x).
Il faut les ajouter pour former C(x).*

En bref, C(x) n'est pas $x^3$ .
'1000' doit être le CRC (à condition que la valeur '1000' soit exacte, bien sûr).

Tu devrais revoir ton cours pour le "mot codé C(x)".
Je crois que tu confonds CRC et 'mot codé'

Lorsque tu auras trouvé correctement C(x), pour prouver que C(x) est multiple de G(x) :

Avec du calcul binaire, tu pourras faire la division euclidienne de C(x) par G(x) et le reste de la division devra être nul

Merci Mtschoon, je vais regarder.

Bonjour, pour revenir sur cet exercice. Je me serai bien trompé sur C(x).
C(x) serait le mot à transmettre (10011101) + le CRC trouvé (1000) soit c(x)=100111011000
La division euclidienne serait entre x³+x⁴+x⁶+x⁷+x⁸+x¹¹ et x⁴+x²+x+1?

Merci

Je viens de la faire en binaire avec 100111011000 par 10111
j'obtiens:

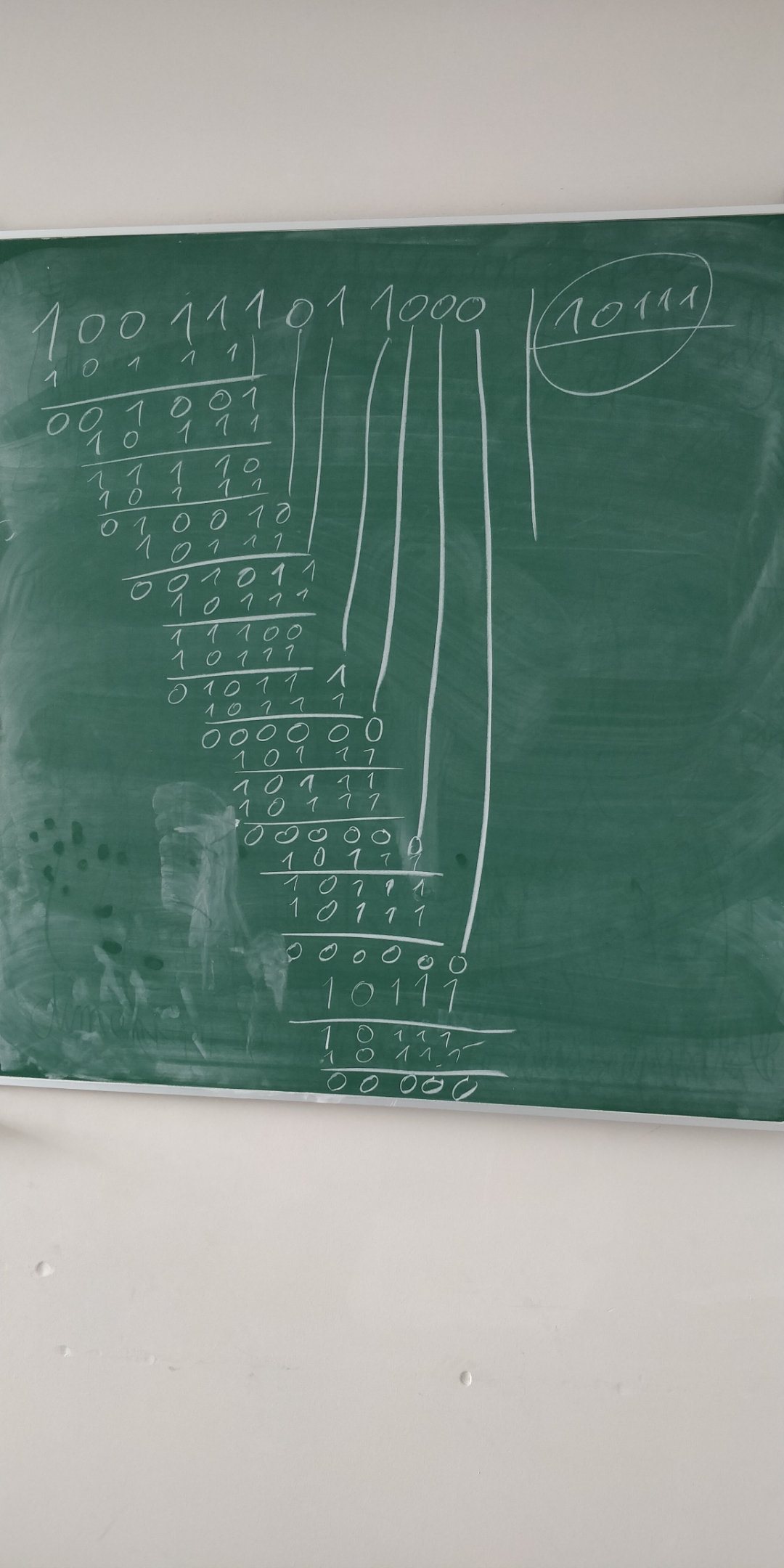
Je ne suis pas sûr de la méthode. Faut il faire les soustraction du bas?

Rebonjour Dut,

Maintenant, ta démarche pour trouver C(x) est bonne.

Je n'ai pas regardé de près ton calcul, mais tu dois t'arrêter lorsque tu as épuisé tous les chiffres du dividende C(x).

Merci beaucoup Mtschoon.
Bonne soirée et à bientôt