La résistance équivalente
-
Ssui dernière édition par sui
Bonjour j'espère que vous allez bien!
Je suis en train de préparer au concours et je me bloque sur cette question qui demande de déterminer la résistance équivalente du dipôle AB
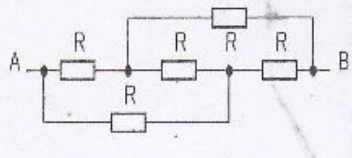
J'ai essayé de appliquer les lois usuelles (Réq=R1+R2 en série ) et (1/Réq=1/R1+1/R2 en parallèle ) mais ça ne semble pas très utile, je ne sais pas si il y a une autre idée ?
Merci d'avance !
-
mtschoon dernière édition par mtschoon

@sui , bonjour,
Je t'indique, si besoin, une version possible pour répondre à ta question.
Je ne suis absolument pas spécialiste en Physique (mes souvenirs datent de plusieurs décennies...), il peut y avoir d'autres méthodes !Je te joins un schéma fait avec Geogebra.
R est représentée par des carrés bleus.
U est la différence de potentielle entre A et B
Les intensités sont I,I1,I2I, I_1, I_2I,I1,I2
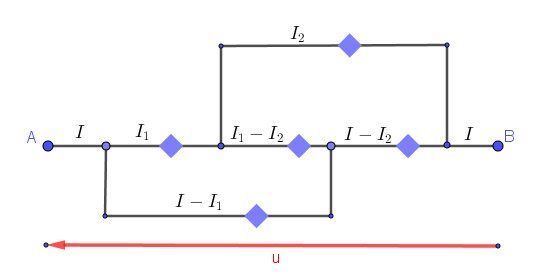
En passant par la branche supérieure, on peut écrire :
U=RI1+RI2U=RI_1+RI_2U=RI1+RI2 (formule 1)
En passant par la branche inférieure, on peut écrire :
U=R(I−I1)+R(I−I2)U=R(I-I_1)+R(I-I_2)U=R(I−I1)+R(I−I2) (formule 2)formule 2 <=> U=2RI−R1I1−RI2U=2RI-R_1I_1-RI_2U=2RI−R1I1−RI2 <=>U=2RI−(RI1+RI2)U=2RI-(RI_1+RI_2)U=2RI−(RI1+RI2)
En utilisant la formule 1
U=2RI−UU=2RI-UU=2RI−U
c'est à dire 2U=2RI2U=2RI2U=2RI, c'est à dire U=RI\fbox{U=RI}U=RILa résistance équivalente vaut donc : $\fbox{R_{eq}=R}$
Remarque ; le "chemin rectiligne" donne une 3ème équation,
Elle n'est pas commode pour répondre à la question.
Evidemment, si des précisions avaient été demandées, elle pourrait être utile.Bon travail.
-
Ssui dernière édition par
Merciii beaucoup @mtschoon!
Au fait, j'ai trouvé la même question mais pour la solution il ont utilisé la loi de kennelly (je pense que c'est du bac+1), mais vraiment votre réponse m'a sauvé
Je ne sais pas ce que je vais faire sans votre aide!
Je peux utiliser la même méthode pour des questions similaires n'est ce pas?
-
mtschoon dernière édition par mtschoon

Contente de t'avoir aidé, @sui

Je ne suis pas professeur de Physique ; la loi de kennelly, ça ne me rappelle rien...
Je viens de regarder sur le web : il s'agit d'une transformation utilisée pour simplifier des circuits comportant des dérivations. Il y a des documents et même des vidéos .
Tu peux consulter si ça fait partie de ton programme.Je t'ai proposé une méthode de lycée (Bac) qui fonctionne bien, qui est logique. et que tu peux utiliser dans d'autres exercices.
Bon courage pour ta préparation de concours !
-
Ssui dernière édition par
Merciii beaucoup @mtschoon!
-
mtschoon dernière édition par

De rien, @sui et bon travail !
-
Ssui dernière édition par sui
Une autre petite question
 concernant le même sujet :
concernant le même sujet :
J'ai été en train de penser si on a par exemple un file à la place d'une de ces deux résistances
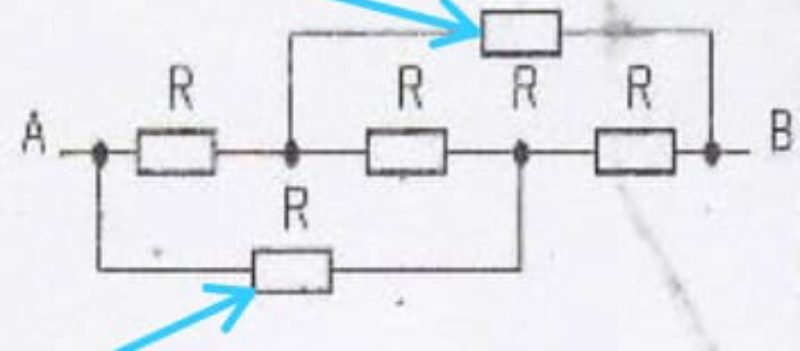
Comment on va trouver la résistance équivalente
Je pense qu'on va passer seulement par les branches qui contient des résistances, est-ce que c'est correct?
-
Ssui dernière édition par
Voilà un exemple qui exprime se que je veux dire
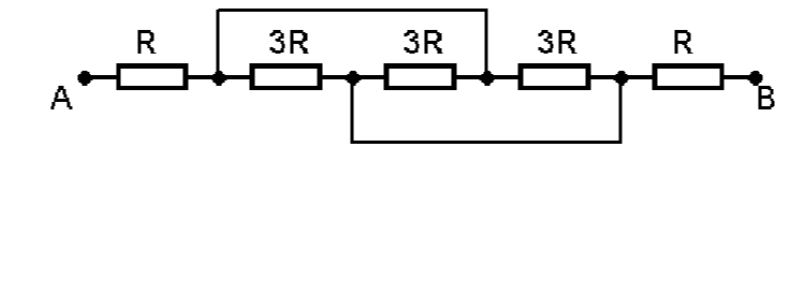
-
mtschoon dernière édition par mtschoon

Pour calculer U, la méthode générale s'applique.
Pour aller de A à B , dans ton dernier schéma, il n'y a pas de chemins sans résistance.
Sur une "partie sans résistance", la différence de potentielle sur cette partie est nulle (0 x Intensité=0)
Bien sûr, comme indiqué, il y a d'autres méthodes pour faire les calculs seulement avec les propriétés des résistances, sans passer par les intensités.
Remarque :
Je viens de faire les calculs avec les intensités.
Dans ce second cas, c'est plus compliqué que dans ton premier système car il faut utiliser les 3 expressions de U.
Je trouve U=3RIU=3RIU=3RI donc Req=3RR_{eq}=3RReq=3R
Je te le rédigerai si tu le souhaites.En prenant directement les propriétés des résistances (en parallèle et en série), on doit trouver la réponse plus rapidement.
-
Ssui dernière édition par sui
J'aimerai bien savoir la méthode en utilisant les propriétés de la résistance (pour le 2ème schéma )

-
BBlack-Jack dernière édition par
Bonjour,
Bonjour,
Dans le cas du second schéma, c'est immédiat.
Les 3 résistances 3R sont en parallèle ...
Et donc la résistance équivalente entre A et B est : Req = R + (1/3)*3R + R = 3R
-
Ssui dernière édition par sui
Merci @Black-Jack
Il sont en parallèle car il y a des noeuds entre ces 3 résistance?
Parce que je ne savais par si je dois calculer comme il sont en série ou en parallèle, ces files étaient un problème pour moi ...
-
mtschoon dernière édition par mtschoon

Bonsoir @sui et bonsoir @Black-Jack ,
Sui, j’essaie de te détailler l’explication pour le second schéma.
Pour mieux comprendre, commence par compléter le schéma que tu as, en nommant les nœuds rencontrés dans le sens de A ver B : C , D, E , F.
Ne touche pas au chemin direct D → E (avec une résistance de 3R)
Regarde le chemin D→C→fil supérieur sans résistance → E
C’est en fait un chemin D→ E avec une résistance de 3R
Tu peux le représenter plus simplement comme je l’ai fait sur le schéma ci dessous que je joins ici (partie supérieure du schéma)Regarde le chemin D→fil inférieur sans résistance → F → E
C’est en fait un chemin D→ E avec une résistance de 3R
Tu peux le représenter plus simplement comme je l’ai fait sur le schéma ci dessous que je joins ici (partie inférieure du schéma)Ainsi représenté, il y a entre D et E, la configuration classique de 3 résistances de 3R en parallèle.
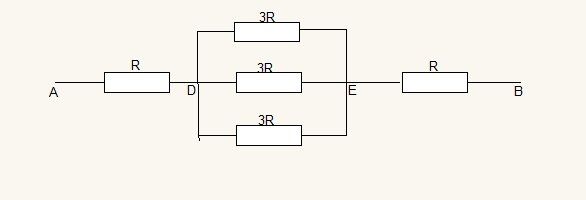
Applique les formules usuelles (elles doivent être dans ton cours)
Soit R’ la résistance équivalente à ces 3 résistances de 3R
1R′=13R+13R+13R\dfrac{1}{R'}=\dfrac{1}{3R}+\dfrac{1}{3R}+\dfrac{1}{3R}R′1=3R1+3R1+3R1Après calcul, tu trouves R′=RR'=RR′=R
Conclusion :
Entre A et B il y a :
une résistance de R (entre A et D), suivie d’une résistance de R (entre D et E), suivie d’une résistance de R (entre E et B)
Ces 3 résistances de R étant en série , en appelant Req leur résistance équivalente :
Req=R+R+R=3RR_{eq}=R +R +R =3RReq=R+R+R=3RReposte si besoin.
-
Ssui dernière édition par
C'est vraiment bien expliqué, merci beaucoup
J'ai jamais pensé à le représenter comme des chemins comme ça
-
mtschoon dernière édition par mtschoon

De rien @sui !
Je n'étais pas sûre que mon explication soit parfaitement claire...
Le piège de cette question était là : visualiser le schéma de façon classique.
Ensuite, les calculs étaient usuels.
-
Ssui dernière édition par
Merciii encore!
-
mtschoon dernière édition par

De rien et bon courage

-
BBlack-Jack dernière édition par
Bonjour,
Pour le problème initial (premier schéma), il y a un chemin rapide vers la solution ... mais je pense qu'il n'est pas accessible aux débutants (et même à beaucoup d'autres ?)
Par la pensée, on enlève la résistance qui est en plein milieu du schéma et on calcule la différence de potentiel aux bornes de cette résistance enlevée.
Par raison de symétrie (ou si on veut par diviseurs de tensions), cette différence de potentielle est nulle.
Donc si on remet la résistance ou n'importe quelle autre valeur de résistance à la place, cela ne change rien (cette résistance sera parcourue par un courant nul)
La résistance équivalente entre A et B peut donc être calculée en remplaçant la résistance centrale soit par un court-circuit, soit par un circuit ouvert.
Le calcul est alors immédiat, suivant le mode de résolution choisi (court-circuit ou ouvert) , on a soit Req = R/2 + R/2 = R, soit Req = 2R // 2R = R
Remarque :
Si on a ce "coup d'oeil", la résistance équivalente est trouvée en quelques secondes, sans véritables calculs.
... Mais, comme déjà dit, ce "coup d'oeil" n'est pas à la portée de tous (et donc ne pas se tracasser si on ne l'a pas).
-
BBlack-Jack dernière édition par
Désolé pour l'orthographe ... je devrais toujours relire avant d'envoyer.

-
Ssui dernière édition par
Merci beaucoup pour votre aide @Black-Jack, Je viens de voir votre réponse et vous avez raison j'ai toujours besoin à faire des calculs pour trouver la solution, et c'est aussi préférable pour moi de faire des calculs pour ne pas avoir des fautes réponses...
(Je fais beaucoup de fautes aussi, ne vous inquiétez pas )
)