Probabilité schéma de Bernoulli/loi binomiale

[dut]

Bonjour Je travaille sur un exemple d'exercice d'annale.

On considère une population dans laquelle en moyenne, on trouve un centenaire pour 1000 personnes. On réunit 1000 personnes choisies au hasard dans cette population. Quelle est la probabilité de trouver au moins un centenaire dans le groupe ? Et dans un groupe de 2000 personnes ?

--> J'ai déduit qu'il fallait appliquer la loi de Bernoulli

Soit un individu est centenaire soit il ne l'est pas
X=1 si centenaire
0 sinon

X suit une loi de Bernoulli de paramètre P: X~B(p)

Après je ne sais pas quoi faire

[mtschoon]

Dut, bonjour,

Un rappel de cours, peut-être, qui te suffira à résoudre ton problème
Épreuve de Bernoulli :
On appelle épreuve de Bernoulli une épreuve n'ayant que deux issues : Succès (S) et Échec(E).
La loi de Bernoulli de paramètre p associe au succés (S) la probabilité p et à l'échec (E) la probabilité (1-p).
Schéma de Bernoulli :
On appelle schéma de Bernoulli, la répétition n fois, de manière indépendante, d'une épreuve de Bernoulli.
Soit X la variable aléatoire correspondant au nombre de succès à l’issue de schéma de Bernoulli.
La loi de probabilité de X est la loi Binomiale de paramètres n et p , notée B(n;p).

Soit B(n ; p) une loi Binomiale.
La probabilité d’obtenir k succès (0≤ k ≤n) est donnée par la formule suivante :
$\fbox{P(X=k)=C(n,k)p^k(1-p)^{n-k}}$
(C(n,k) représente le nombre de combinaisons de k éléments choisis parmi n

Essaie de voir si avec ce rappel tu arrives à faire l'exercice, sinon reposte.

[dut]

Alors cela donne B(1000, P)
P(au moins 1 centenaire) =(1000, >=1) (1/1000)*.....

Comment faire pour définir la valeur de P? c'est bien ce qu'on cherche?

[mtschoon]

La loi binomiale X à utiliser est bien B(n,p) avec n=1000 et p=1/1000.
Tu cherches la probabilité de trouver au moins un centenaire dans le groupe de 1000 personnes.

Je te conseille de passer par l'évènement contraire : la probabilité de trouver aucun centenaire dans le groupe
Tu prends la formule encadrée dans ma réponse précédente et tu remplaces k par 0
$P(X=0)=C(n,0)p^0(1-p{)}^n=1\times 1\times (1-p{)}^n$
$P(X=0)=0.999^{1000}$

La probabilité de trouver au moins un centenaire dans le groupe est donc $P(X\ge 1)$

$P(X\ge 1)=1-P(X=0)=1-0.999^{1000}$

Pour le groupe de 2000 personnes, n change.
n vaut 2000 au lieu de 1000 mais p=1/1000 reste le même.
Même principe.

[dut]

Merci Mtschoon
Je me demande pourquoi il est préférable par l'événement contraire. Cela est -il normalement plus intuitif ?

Je n'ai pas compris comment de P(X=0)= C(n,0)p⁰(1-p)p^n= 11(1-p)^n

Sinon je pense que c'est plus clair.
Je trouve pour le 1er cas : 63% et pour le second 86%

[mtschoon]

Si tu utilisais "au moins un" tu aurais 999 probabilités à ajouter
$P(X\ge 1)=P(X=1)+P(X=2)+...+P(X=1000)$
(en appliquant 999 fois la formule encadrée... )

En passant par P(X=0) il n'y a qu'un cas et en plus très simple.

Pour P(X=0) , tu prends par formule $P(X=k)$ et tu remplaces k par 0
$C(n,0)=1$
$p^0=$1
$1-p=1-0.001=0.999$
$n-0=n$

Précise ce qui te gène.

[mtschoon]

Tu as écris "Je trouve pour le 1er cas : 63% et pour le second 86%"

Je ne vois pas d'où peuvent sortir ces réponses...

1er cas : pour n=1000 , la réponse est $1-0.999^{1000}$
2eme cas : pour n=2000, la réponse est $1-0.999^{2000}$
Ma calculette n'a pas assez de puissance pour calculer ces expressions.

[dut]

ce qui me gène c'est principalement C(n,0) =1

[mtschoon]

C(n,k) est le nombre de façons de choisir k éléments parmi n
C(n,0) est le nombre de façons de choisir 0 élément parmi n.
En bref, il y a une seule façon : ne rien choisir
donc C(n,0)=1

Il y a une formule générale avec les C(n,k)
Tu l'as peut-être dans ton cours et tu peux remplacer k par 0, mais je ne pense pas que ça te soit utile pour ton exercice.
$C(n,k)=\frac{n!}{k!(n-k)!}$

[dut]

Merci Mtschoon
Donc 63% de chance d'avoir au moins 1 centenaire dans un groupe de 1000 et 86% dans un groupe de 2000

[dut]

Pardon je n'avais pas vu le second message
Je trouve ces valeurs en fais 1-0,999^1000

[mtschoon]

C'est bon Dut.

Bonne soirée !

[dut]

Bonjour Mtschoon,
Je ne comprends pas si les pourcentages donnés sont bons ou pas

[mtschoon]

Bonjour Dut,

Si tu parles de tes réponses
" 63% de chance d'avoir au moins 1 centenaire dans un groupe de 1000 et 86% dans un groupe de 2000", j'ignore toujours comment tu les as calculées..
ma calculette n'est pas assez puissante pour calculer avec les formules écrites, donc je n'ai pas cherché les valeurs autrement.
Je vais passer par les logarithmes pour voir si elle pourra y arriver et je te tiens au courant.

[dut]

1-0,999^1000= 0,63 *100 =63 %

Je sais que nous n'auront pas de calculette pour le contrôle et que ce tableau nous est donné:

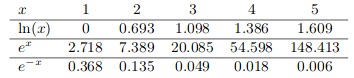
Comment grâce à ce tableau je peux arriver à retrouver le 0,63. C'est plus la démarche qu'il me manque parce que je pense que pour retomber sur 0,63 il faut faire 1 - 0,368

[mtschoon]

Ca y est.
J'ai fini par faire "cracher" des valeurs à ma calculette en passant par logarithmes et exponentielles !
Tes réponses sont bonnes car j'arrive à 63,23% et 86,48% avec mes "manipulations" !
Tu dois avoir une "super calculette" si elle a pu faire le calcul sans sourciller. La mienne bloque sur l'exposant 1000 ...

[mtschoon]

Tu aurais pu préciser que tu avais un tableau !

rappels indispensables à savoir :
pour x > 0 et a>0, $\fbox{e^{ln(x)}=x}$ et $\fbox{a^x=e^{xlna}}$ et $\fbox{ln(a^x)=xlna}$

Je t'indique la démarche que j'ai utilisé pour trouver une valeur approchée de $0.999^{1000}$ puis de $1-0.999^{1000}$ avec ma calculette (qui ne peut pas effectuer des puissances 1000, ni 2000...)

$\fbox{ln(0.999^{1000})=1000\ln(0.999)}$

Ma calculette me donne $ln(0.999)\approx -0.001001$

En multipliant par 1000 : $1000ln(0.999)\approx -1.001$

En prenant l'exponentielle : $e^{1000ln(0.999)}\approx 0.3675...$

c'est à dire $0.999^{1000}\approx 0.3675$

au final

$1-0.999^{1000}\approx 1-0.3675$

$1-0.999^{1000}\approx 63.25$

Vois avec ton tableau.

Les résultats que tu as proposés sont bons.

[dut]

Merci Mtschoon
J'ai découvert le tableau ce matin en ouvrant une annale.
J'en pleurs de désespoir la partie est loin d’être gagnée je bloque à tous les exercices de l'annale

[mtschoon]

Je t'indique comment tu peux utiliser le tableau, mais il faut connaitre encore des propriétés des logarithmes...

Soit $x=0.999^{1000}$

$x=e^{1000ln(0.999)}$

Il faut transformer ln(0.999)

Propriété à savoir: pour x voisin de 0, $\fbox{ln(1+x)\approx x}$ et $\fbox{ln(1-x)\approx -x}$
Or $ln(0.999)=ln(1-0.001)$
Donc $ln(0.999)\approx -0.001$

En multipliant par 1000 : $1000ln(0.999)\approx -1$

donc $x\approx e^{-1}$

Avec le tableau joint : $x\approx 0.368$

et évidemment $1-0.368=0.632$ d'où environ les 63% cherchés.

(même principe avec 2000 au lieu de 1000)

[mtschoon]

En bref, quelle que soit la méthode, tu ne peux pas échapper aux propriétés des logarithmes et exponentielles.
Je te mets un lien, mais évidemment, il faut du temps pour assimiler tout ça....
https://www.mathforu.com/terminale-s/fonctions-exponentielles-et-logarithme-pour-terminale-s/

Comme nous te l'avons toujours dit, ce qu'il faudrait, c'est pouvoir consolider tes connaissances de base.
Bien sûr, c'est plus facile à dire qu'à faire...

Mais, il n'y a pas que les maths, j'imagine, dans ta préparation.
De toute façon, dis toi que tu as ta conscience pour toi et que tu fais le maximum . C'est l'essentiel.

[dut]

Merci beaucoup pour votre aide et pour votre petit message.

[mtschoon]

De rien Dut, et bon travail .