Besoin d'aide dm de math stmg

Bonjour j'ai besoin d'aide urgent pour un exercice de math niveau 1er STMG
Sujet F:
Soit $f$ la fonction définie sur R par $f(x) = 2x^2+5x-3$ .
On note C la représentation graphique de f dans le plan rapporté à un repère orthonormé.
1.a. Vérifier que -3 est une racine de $f (x)$
b. En déduire le polynôme $f (x)$ sous forme factorisée
2.a. étudié les variations de la fonction f et dresser son tableau de variation
b. En utilisant les variation de f , déterminer les valeurs du réel k telles que l'équation f(x)=k n'ait aucune solution
3.a représenter graphiquement $f$
b. Résoudre graphiquement l'équation $f (x) = 3$
c. Résoudre graphiquement l'inéquation $f (x)$ <ou=1.

Merci d'avance
Ps(c'est vraiment urgent)

Expressions mathématiques écrites en Latex par la modération

@Oasix-pandaroux , bonjour,

Tu as fait, je suppose, une faute de frappe dans ton énoncé

C'est, je pense, $f(x)=2x^2+5x-3$

Piste pour démarrer,

1)a) tu calcules f(-3) et tu dois trouver f(-3)=0

$f(-3)=2(-3)^2+5(-3)-3=2(9)-15-3=...$ (tu comptes)

1)b)
D'après la réponse de la 1)a), tu peux déduire que -3 est une racine de f(x)
Il faut trouver l'autre racine.
Il y a plusieurs méthodes, mais il faut que tu indiques ce que tu as vu en cours.

Tu peux bien sûr résoudre l'équation $2x^2+5x-3=0$ avec les formules de résolution, mais cela n'est pas dans l'esprit de l'exercice car dans ce cas la première question ne servirait à rien.
Peut-être connais tu le produit des racines ou la somme ?
Il faut que tu le dises.
La seconde racine est 1/2=0.5.

@mtschoon merci cette réponse c'est pour les 2 premier ?

@Oasix-pandaroux ,

Comme je te l'ai indiqué, c'est pour 1)a) et 1)b) (le début)

@mtschoon ok merci beaucoup tu aurais une piste pour les autre question ?

@Oasix-pandaroux ,

Tu n'as pas indiqué comment tu as l'habitude de trouver l'autre racine d'une équation du second degré, lorsqu'on en connait une.

@mtschoon c'est parce que je ne sais pas le faire

@Oasix-pandaroux

Il est très difficile de t'aider si l'on ne sais pas le contenu de ton cours...

Si tu sais (?) que le produit des racines $x_1$ et $x_2$ d'une équation du second degré $ax^2+bx+c=0$ est $\fbox{x_1\times x_2=\dfrac{c}{a}}$ , tu peux trouver $x_2$

ici, $x_1=-3$ , $a = 2$ et $c = - 3$
Tu peux ainsi trouver que $x2=12x_2=\dfrac{1}{2}$

Méthode pour factoriser $f(x)=ax^2+bx+c$

$x_1$ et $x_2$ étant les racines du polynôme
$\fbox{f(x)=a(x-x_1)(x-x_2)}$

Ici, $a = 2$ , $x_1=-3$ et $x_2=1/2$

@mtschoon ok merci tu me sauves j'arriverais a faire la suite je pense

@Oasix-pandaroux , de rien !

Si besoin, je te joins un graphique qui peut te permettre de vérifier tes réponses.

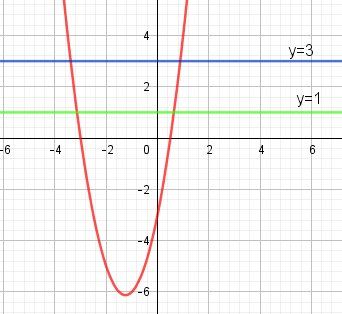
Bon travail.

@mtschoon merci bien grâce a vous j'ai terminé a temps