Recherche sur calcul intégral
-
Wil Fried dernière édition par

J'ai besoin d'aide pour cet exercice svp
Intégral allant de 0 à pi/2 de Ln(sinx)dx.
Calculer cet intégral
-
mtschoon dernière édition par mtschoon

@Wil-Fried , bonsoir,
Bien sûr, ce genre d'intégrale ne se calcule pas de façon usuelle. mais celle ci est assez classique
Sauf erreur, elle vaut −π2ln2-\dfrac{\pi}{2}ln2−2πln2
Je te joins deux vidéos qui la calcule.
Elles ne sont pas en français et un peu fatigantes à entendre mais on peut suivre les calculs.
-
Wil Fried dernière édition par

@mtschoon merci beaucoup monsieur!
Je faisais des recherches et je suis tombé dessus donc j'aimerai savoir calculer ce genre.
-
mtschoon dernière édition par

De rien @Wil-Fried ,
Ce n'est pas monsieur, c'est "madame" mais aucune importance, et bonne lecture.
-
Wil Fried dernière édition par

@mtschoon oups!! Excusez moi!
-
mtschoon dernière édition par

@Wil-Fried , pas de problème !
-
mtschoon dernière édition par mtschoon

Quelques pistes pour éclairer, peut-être, le calcul de I=∫0π2ln(sinx)dx\displaystyle\boxed{ I=\int_0^{\dfrac{\pi}{2}}ln(sinx)dx}I=∫02πln(sinx)dx
Soit f(x)=ln(sinx)f(x)=ln(sinx)f(x)=ln(sinx) d'où f′(x)=cosxsinxf'(x)=\dfrac{cosx}{sinx}f′(x)=sinxcosx
Tableau de variation sur ]0,π[]0,\pi[]0,π[
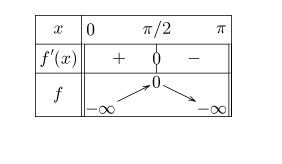
Représentation graphique sur ]0,π[]0,\pi[]0,π[
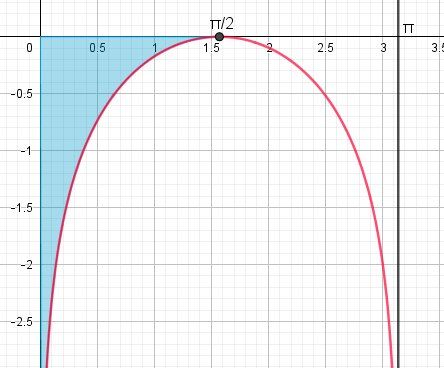
I représente "l'aire algébrique" (ici négative) de la zone coloriée.
-
mtschoon dernière édition par mtschoon

I=∫0π2ln(sinx)dx\displaystyle I=\int_0^{\dfrac{\pi}{2}}ln(sinx)dxI=∫02πln(sinx)dx
(intégrale "impropre" convergente)Soit J=∫0π2ln(cosx)dx\displaystyle J=\int_0^{\dfrac{\pi}{2}}ln(cosx)dxJ=∫02πln(cosx)dx
Changement de variable x=π2−tx=\dfrac{\pi}{2}-tx=2π−t d'où dx=−dtdx=-dtdx=−dt
I=∫π20ln(sin(π2−t)(−dt)=∫0π2ln(cost)dt\displaystyle I=\int_{\dfrac{\pi}{2}}^0 ln(sin(\dfrac{\pi}{2}-t)(-dt)=\int_0^{\dfrac{\pi}{2}}ln(cost)dtI=∫2π0ln(sin(2π−t)(−dt)=∫02πln(cost)dtDonc I=JI=JI=J
Conséquence:
I+J=2I=∫0π2ln(sinx)dx+∫0π2ln(cosx)dxI+J=2I=\int_0^{\dfrac{\pi}{2}}ln(sinx)dx+\int_0^{\dfrac{\pi}{2}}ln(cosx)dxI+J=2I=∫02πln(sinx)dx+∫02πln(cosx)dx2I=∫0π2[ln(sinx)+ln(cosx)]dx\displaystyle 2I=\int_0^{\dfrac{\pi}{2}}[ln(sinx)+ln(cosx)]dx2I=∫02π[ln(sinx)+ln(cosx)]dx
2I=∫0π2ln(sinxcosx)dx=∫0π2ln(12sin(2x))dx\displaystyle 2I=\int_0^{\dfrac{\pi}{2}}ln(sinxcosx)dx=\int_0^{\dfrac{\pi}{2}}ln\biggl(\dfrac{1}{2}sin(2x)\biggl)dx2I=∫02πln(sinxcosx)dx=∫02πln(21sin(2x))dx
2I=∫0π2ln12dx+∫0π2ln(sin(2x))dx\displaystyle 2I=\int_0^{\dfrac{\pi}{2}}ln\dfrac{1}{2}dx+\int_0^{\dfrac{\pi}{2} }ln(sin(2x))dx2I=∫02πln21dx+∫02πln(sin(2x))dx
Soit K=∫0π2ln12dx\displaystyle K=\int_0^{\dfrac{\pi}{2}}ln\dfrac{1}{2}dxK=∫02πln21dx =[ln12x]0π2=π2ln12=−π2ln2\biggl [ln\dfrac{1}{2}x \biggl]_0^{\dfrac{\pi}{2}}=\dfrac{\pi}{2}ln\dfrac{1}{2}=-\dfrac{\pi}{2}ln2[ln21x]02π=2πln21=−2πln2
Soit L=∫0π2ln(sin(2x))dx\displaystyle L=\int_0^{\dfrac{\pi}{2}}ln(sin(2x))dxL=∫02πln(sin(2x))dx
Changement de variable u=2xu=2xu=2x d'où du=2dxdu=2dxdu=2dx
L=∫0πln(sinu)12du=12∫0πln(sinu)du\displaystyle L=\int_0^{\pi }ln(sinu)\dfrac{1}{2}du=\dfrac{1}{2}\int_0^{\pi }ln(sinu)duL=∫0πln(sinu)21du=21∫0πln(sinu)du
L=12∫0π2ln(sinu)du+12∫π2πln(sinu)du\displaystyle L=\dfrac{1}{2}\int_0^{\dfrac{\pi }{2}}ln(sinu)du+\dfrac{1}{2}\int_{\dfrac{\pi}{2}}^{\pi}ln(sinu)duL=21∫02πln(sinu)du+21∫2ππln(sinu)du
L=12I+12IL=\dfrac{1}{2}I+\dfrac{1}{2}IL=21I+21I (voir axe de symétrie d'équation x=π2x=\dfrac{\pi}{2}x=2π, de la courbe représentée)
L=IL=IL=I
CONCLUSION
Vu que 2I=K+L2I=K+L2I=K+L, on déduit 2I=−π2ln2+I2I=-\dfrac{\pi}{2}ln2+I2I=−2πln2+I
Et enfin I=−π2ln2\boxed{I=-\dfrac{\pi}{2}ln2}I=−2πln2
CQFD.
-
Wil Fried dernière édition par

@mtschoon waoo!! Merci beaucoup! Je reprendrai seul pour vérifier ma compréhension.
-
Wil Fried dernière édition par

@mtschoon J'ai deux questions svp !
La première.. Pourquoi vous avez fait sorti une nouvelle intégrale «J» ?
La deuxième.. Pourquoi avoir choisi de poser que x =( pi/2)-t en particulier ?
-
mtschoon dernière édition par mtschoon

@Wil-Fried , bonjour,
Très bonne idée de reprendre seul la démonstration

Pour ta première question.
Les fonctions sin et cos sont de "même nature"
L'intégrale de ln(sin(x)) et l'intégrale de ln(cos(x)) sont aussi de même nature.Si on regarde graphiquement ces intégrales, sans calcul, on constate qu'elles sont égales
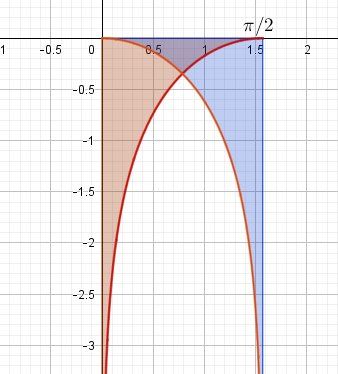
Bien sûr, il faut le démontrer mathématiquement.Calculer l'une revient à calculer l'autre.
L'astuce de la démonstration générale est de calculer I+J ( qui vaut 2I ) pour pouvoir faire des transformations en utilisant les propriétés du logarithme (lna+lnb=ln(ab) et les propriétés trigonométriques (formule de duplication sin(2a)=2sinacosa, c'est à dire sinacosa=(1/2)sin(2a)
Ensuite, tout le reste des calculs s'en déduit.Pour ta seconde question
Il faut démontre mathématiquement que J=I
IL faut donc transformer un cosinus en sinus
La méthode la plus simple est d'utiliser les angles complémentaires.
(Pour faire court, dans tout triangle rectangle, les deux angles aigus sont complémentaires (leur somme vaut π\piπ/2). Le cosinus de l'un est égal au sinus de l'autre)En posant x=π2−tx=\dfrac{\pi}{2}-tx=2π−t, sinxsinxsinx, qui vaut ainsi sin(π2−t)sin(\dfrac{\pi}{2}-t) sin(2π−t) se transforme en costcostcost
J'espère avoir répondu à tes deux questions.
Contente que cette intégrale , assez classique, mais qui finalement se calcule sans trop de difficultés (à condition de pense à une bonne stratégie) , t'intéresse.
-
GGuillaume.87 dernière édition par Guillaume.87
Bonjour,
En attendant une réponse peut-être plus détaillée de @mtschoon , je me permets de te répondre pour t'aider en attendant. Tu l'as compris, cette intégrale III ne se calcule pas directement avec une primitive : il faut donc ruser, et "contourner le calcul" en raisonnant par égalités successives pour aboutir à un résultat chiffré de cette intégrale.
L'intégrale JJJ est en réalité l'intégrale III, c'est tout à fait la même chose comme le prouve la 5ème ligne de la démonstration de @mtschoon . Cette intégrale JJJ est donc une autre façon d'écrire l'intégrale III, ce qui permettra ensuite d'utiliser les propriétés algébriques de la fonction lnlnln et les formules trigonométriques en additionnant III et JJJ : ainsi, on obtiendra un premier résultat préliminaire.
-
mtschoon dernière édition par mtschoon

-
GGuillaume.87 dernière édition par
@mtschoon
Oui tout à fait,J'étais en train d'écrire la suite mais je me suis arrêté en voyant que tu avais posté ta réponse. je te laisse donc finir tes explications !

Bonne journée à toi
-
mtschoon dernière édition par

J'espère que mes explications complémentaires suffiront à @Wil-Fried .
-
Wil Fried dernière édition par

@mtschoon Je vous remercie infiniment vous et @Guillaume-87 pour vos éclairages. Je vais refaire et s'il y a encore des zones d'ombres vous revenir pour plus d'éclaircissements!
Merci encore!
-
mtschoon dernière édition par

@Wil-Fried , d'accord, revient si nécessaire et bons calculs !