Intersections de cercles
-
PPoddon28 dernière édition par
Bonjour à tous,
Je suis nouveau sur le forum et je fais appel à vos lumières car je suis un peu rouillé en calcul. J'espère adresser ma question au bon endroit du forum.
Le problème que je cherche à résoudre est le suivant: calculer la distance d entre deux cercles de rayons R telle que la surface d'intersection de ces deux cercles soit égale à la valeur S.
Après quelques recherches, je pense avoir exprimé S en fonction de R et d:
S=2R.cos−1(d2R)−12d4R2−d2S = 2R.cos^{-1}(\frac{d}{2R})-\frac{1}{2}d\sqrt{4R^2-d^2}S=2R.cos−1(2Rd)−21d4R2−d2
Je souhaiterais maintenant exprimer d en fonction des autres facteurs de l'équation (d étant la seule inconnue). J'ai essayé de triturer cette expression pour simplifier le cos-1 ou éliminer la racine, sans parvenir au résultat voulu.
Cela fait un certain temps que je n'ai pas travaillé ce type de manipulation, est ce que quelqu'un pourrait me mettre sur la piste d'une méthode permettant de résoudre mon problème ?
Merci d'avance et bonne journée !
-
mtschoon dernière édition par mtschoon

@Poddon28 , bonjour,
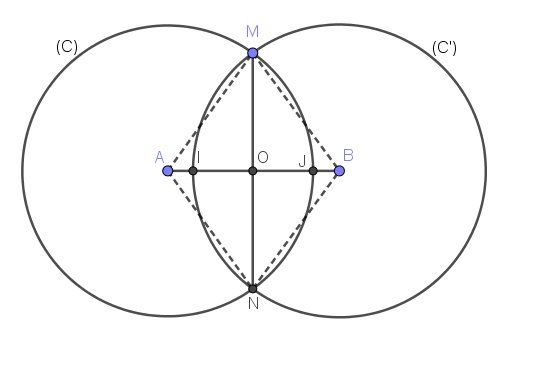
Pour la formule que tu indiques, il manque un carré à R
S=2R2cos−1(d2R)−dR2−(d2)2\boxed{S=2R^2cos^{-1}\biggl(\dfrac{d}{2R}\biggl)-d\sqrt{R^2-\biggl(\dfrac{d}{2}\biggl)^2}}S=2R2cos−1(2Rd)−dR2−(2d)2
Avec cette formule, trouver d en fonction de R et S me parait mission impossible vu que d intervient à la fois sous le radical et dans le cos−1cos^{-1}cos−1Tu peux éventuellement y arriver , de façon indirecte, en faisant intervenir l'angle α=NAM^\alpha=\widehat{NAM}α=NAM , c'est à dire α2=OAM^\dfrac{\alpha}{2}=\widehat{OAM}2α=OAM
Ce ne sera pas miraculeux car il faudra trouver une valeur approchée de α\alphaα pour poursuivre les calculs numériquement.
Je t'indique cette possibilité.
S2\dfrac{S}{2}2S, aire de la demi -lentille, vaut :
aire(ONJM)=R22(α−sinα)aire (ONJM)=\frac{R^2}{2}(\alpha-sin \alpha)aire(ONJM)=2R2(α−sinα)
(Tu peux le prouver facilement)S2=R22(α−sin(α))\dfrac{S}{2}=\frac{R^2}{2}(\alpha-sin(\alpha))2S=2R2(α−sin(α)) <=> sinα=α−SR2sin\alpha=\alpha-\dfrac{S}{R^2}sinα=α−R2S
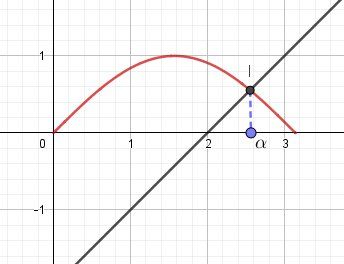
α\alphaα est solution de sinx=x−SR2sinx=x-\dfrac{S}{R^2}sinx=x−R2S
Tu peux trouver une valeur approchée de α\alphaα par méthode graphique ou par approximation numériqueGraphiquement, en représentant la fonction f définie par f(x)=sinxf(x)=sinxf(x)=sinx pour 0≤x≤π0\le x\le \pi0≤x≤π et la fonction g définie par g(x)=x−SR2g(x)=x-\dfrac{S}{R^2}g(x)=x−R2S, on obtient :
Ensuite, vu que
d2R=2AO2AM=AOAM=cos(α2)\dfrac{d}{2R}=\dfrac{2AO}{2AM}=\dfrac{AO}{AM}=cos(\dfrac{\alpha}{2})2Rd=2AM2AO=AMAO=cos(2α),cos−1(d2R)=α2cos^{-1}(\dfrac{d}{2R})=\dfrac{\alpha}{2}cos−1(2Rd)=2α
S=R2α−dR2−(d2)2S=R^2\alpha-d\sqrt{R^2-\biggl(\dfrac{d}{2}\biggl)^2}S=R2α−dR2−(2d)2
Avec cette formule , tu peux "triturer", comme tu dis, pour trouver d :
Tu isoles l'expression contenant d
dR2−(d2)2=R2α−Sd\sqrt{R^2-\biggl(\dfrac{d}{2}\biggl)^2}=R^2\alpha-SdR2−(2d)2=R2α−S
Tu élèves les deux membres de l'équation au carré
Tu obtiens ainsi une équation bicarrée de la forme
ad4+bd2+c=0ad^4+bd^2+c=0ad4+bd2+c=0
Tu fais le changement d'inconnue D=d2D=d^2D=d2
Equation auxiliaire : aD2+bD+c=0aD^2+bD+c=0aD2+bD+c=0
Tu résous cette équation du second degré d'inconnue D
Tu conserves la solution D1D_1D1 vérifiant 0≤D1≤4R20\le D_1\le 4R^20≤D1≤4R2
D'où réponse : d1=D1d_1=\sqrt D_1d1=D1Evidemment, la précision du résultat pour d dépend de la précision trouvée par α\alphaα...mais faute de mieux...
Bons calculs !
-
PPoddon28 dernière édition par Poddon28
Bonjour mtschoon, et merci pour cette réponse détaillée.
Effectivement, j'avais oublié un carré dans l'expression de la surface de recouvrement.
Je vais essayer de reprendre ta proposition afin de bien comprendre toutes les étapes.Dans la méthode que tu propses, il y a une étape de résolutions graphique ou numérique pour déterminer α\alphaα. Pour cela, tu as tracé sin(x)sin(x)sin(x) et une fonction g(x)=x−SR2g(x)=x-\frac{S}{R^2}g(x)=x−R2S. J'en déduis que tu as fixé (arbitrairement?) une valeur pour le rapport SR2\frac{S}{R^2}R2S ( SR2=2\frac{S}{R^2}=2R2S=2)? Qu'est ce que cela conditionne sur la suite de la résolution ?
Le weekend étant passé par là, j'ai discuté du problème avec un amis qui m'a proposé la méthode suivante:
- Tracer la fonction S(d)=2R2.cos−1(d2R)−12d(4R2−d2)S(d)=2R^2.cos^{-1}(\frac{d}{2R})-\frac{1}{2}d\sqrt{(4R^2-d^2)}S(d)=2R2.cos−1(2Rd)−21d(4R2−d2)
- Trouver une fonction g qui approche la fonction S(d)S(d)S(d) à l'aide d'un tableur
- Utiliser cette fonction g pour calculer d en fonction des valeurs de S qui m'intéressent, en ne prenant que les solutions sur l'intervalle de définition de la fonction S(d)S(d)S(d).
Il apparait qu'un polynôme de degré 2 permet d'approcher assez bien la fonction S(d)S(d)S(d). Il est ensuite assez simple de retrouver les racines de ce polynôme pour une valeur de S donnée.
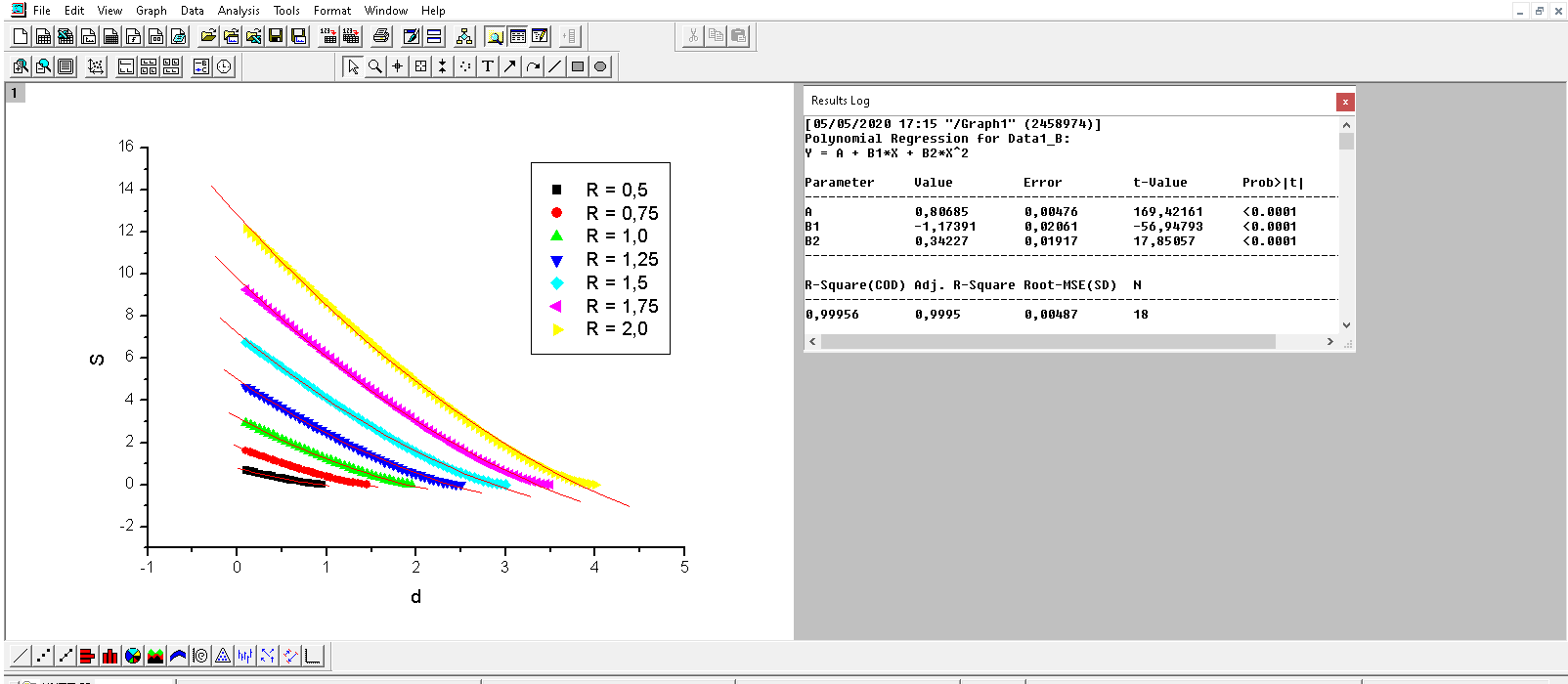
Il me semble que la méthode fonctionne et est suffisante dans mon cas car seules quelques valeurs de d en fonction de S m'intéressent.
Est ce que cette approche serait également valable ?A la lumière de la solution que tu proposes (une solution en d4d^4d4), je me dit qu'approcher la fonction S(d)S(d)S(d) à l'aide d'un polynôme de degré 4 serait encore plus juste et ne complexifierait pas outre mesure la méthode de résolution.
Bonne fin de journée à tous!
-
mtschoon dernière édition par mtschoon

@Poddon28 , bonjour,
Merci pour ton intéressante réponse.
Pour la méthode proposée par tes amis, si j'ai bien lu, tu approches la fonction S par une fonction polynôme du second degré.
Pourquoi pas ?
Tout dépend de la précision sur d que tu souhaites.La proposition que je t'ai faite est plus "mathématique".
Je t'ai donné un exemple d'illustration graphique pour éclairer la méthode.
Bien sûr, j'aurais pu poser, sur [0,π][0,\pi][0,π], h(x)=sinx−x+SR2h(x)=sinx-x+\dfrac{S}{R^2}h(x)=sinx−x+R2S et trouver α\alphaα solution de h(x)=0h(x)=0h(x)=0 (α\alphaα abscisse du point d'intersection de la courbe avec l'axe des abscisses).
Une simple lecture graphique de α\alphaα ne me parait guère précise. C'est bon seulement pour trouver l'ordre de grandeur.
Tu peux utiliser un tableur, ou la fonction TABLE de la calculette.
Mieux, tu peux utiliser une méthode d'approximation d'une solution d'une équation numérique réelle (dichotomie ou Lagrange ou Newton), pour obtenir une valeur de α\alphaα très précise d'où d très précise, mais cela demande un travail certain !
A toute fin utile, je te mets un lien pour cela :
http://epsilon.2000.free.fr/capes/eqnum.pdfA toi de voir en fonction de tes besoins.
Bons calculs et bonne journée
