Utilisation de la Méthode Monté-Carlo
-
FANSI Léo dernière édition par FANSI Léo
Bonjour à tous le monde, j'espère que vous vous portez tous bien malgré la crise liée au COVID-19.

D'autre part, j'espère également être dans le bon groupe pour poser mon problème. Bon voilà, j'ai un exercice en processus stochastique et je suis un peu bloqué parce que j'ai pas bien compris cette partie du cours. L'énoncé en question c'est :**On considère un demi-cercle dans lequel est inscrit le triangle rectangle ABC. Le point B se projette sur le diamètre AC en H tel que AH = HO où O est le centre du cercle (et milieu de AC). On prendra R = OA = OB = 1 unité de longueur.
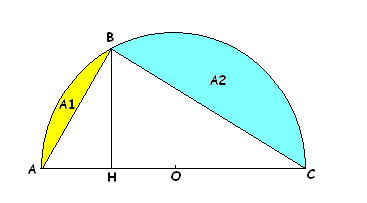
Déterminer une valeur approchée des aires A1 et A2 des segments de cercle jaune et bleu. On décrira avec détails la méthode employée.
Comparer avec le résultat exact.
Les valeurs exactes de A1 et A2 sont 0,091 et 0,614 respectivement et leur somme est 0,70477**Comme je l'ai dit j'ai pas vraiment compris cette partie du cours donc toute aide sera la bienvenue. Merci d'avance!
-
mtschoon dernière édition par mtschoon

@FANSI-Léo , bonjour,
Les valeurs de A1 et A2 que tu indiques ne sont pas les valeurs exactes.
Si tu veux faire du calcul intégral :
L'équation du demi-cercle est y=1−x2y=\sqrt{1-x^2}y=1−x2
L'équation de la droite (AB) est y=3x+3y=\sqrt{3}x+\sqrt 3y=3x+3
L'équation de la droite (BC) est y=−33x+33y=-\dfrac{\sqrt 3}{3}x+\dfrac{\sqrt 3}{3}y=−33x+33A1=∫−1−121−x2dx−∫−1−12(3x+3)dx\displaystyle A_1=\int_{-1}^{-\dfrac{1}{2}} \sqrt{1-x^2}dx-\int_{-1}^{-\dfrac{1}{2}}(\sqrt{3}x+\sqrt 3) dx A1=∫−1−211−x2dx−∫−1−21(3x+3)dx
Avec les primitives usuelles, sauf erreur, après calculs, tu dois trouver
A1=π6−34\boxed{A_1=\dfrac{\pi}{6}-\dfrac{\sqrt 3}{4}}A1=6π−43
0,091 est seulement la valeur approchée de A1A_1A1, à 10−310^{-3}10−3 près, par excès.De même,
A2=∫−1211−x2dx−∫−121(−33x+33)dx\displaystyle A_2=\int_{-\dfrac{1}{2}}^1 \sqrt{1-x^2}dx-\int_{-\dfrac{1}{2}}^1(-\dfrac{\sqrt 3}{3}x+\dfrac{\sqrt 3}{3})dx A2=∫−2111−x2dx−∫−211(−33x+33)dx
Avec les primitives usuelles, sauf erreur, après calculs, tu dois trouver
A2=π3−34\boxed{A_2=\dfrac{\pi}{3}-\dfrac{\sqrt 3}{4}}A2=3π−43
0,614 est seulement la valeur approchée de A2A_2A2 à 10−310^{-3}10−3 près, par défaut.Tu peux trouver des valeurs approchées des intégrales puis des deux aires A1A_1A1 et A2A_2A2 avec la méthode de Monté-Carlo , mais il faut faire un programme informatique pour que ça puisse donner des valeurs approchées convenables...
Je te mets un lien vers une explication très simple de la méthode avec un exemple de programme fait en Python.
Ce n'est peut-être pas le langage Python qui t'intéresse mais ça te permettra, j'espère, de comprendre la démarche.
https://www.youtube.com/watch?v=unkh3TZU3YM
Ensuite, il te faudra l'adapter au langage de programmation dont tu as l'habitude.
-
FANSI Léo dernière édition par
@mtschoon , bonjour et surtout merci pour ton intervention. Tu me sors une épine du pied. Je vais tout de suite regarder la vidéo sur la méthode Monté-Carlo. Encore merci!!



-
LEFAJELE LEFAJELE dernière édition par

@mtschoon a dit dans Utilisation de la Méthode Monté-Carlo :
@FANSI-Léo , bonjour,
Les valeurs de A1 et A2 que tu indiques ne sont pas les valeurs exactes.
Si tu veux faire du calcul intégral :
L'équation du demi-cercle est y=1−x2y=\sqrt{1-x^2}y=1−x2
L'équation de la droite (AB) est y=3x+3y=\sqrt{3}x+\sqrt 3y=3x+3
L'équation de la droite (BC) est y=−33x+33y=-\dfrac{\sqrt 3}{3}x+\dfrac{\sqrt 3}{3}y=−33x+33A1=∫−1−121−x2dx−∫−1−12(3x+3)dx\displaystyle A_1=\int_{-1}^{-\dfrac{1}{2}} \sqrt{1-x^2}dx-\int_{-1}^{-\dfrac{1}{2}}(\sqrt{3}x+\sqrt 3) dx A1=∫−1−211−x2dx−∫−1−21(3x+3)dx
Avec les primitives usuelles, sauf erreur, après calculs, tu dois trouver
A1=π6−34\boxed{A_1=\dfrac{\pi}{6}-\dfrac{\sqrt 3}{4}}A1=6π−43
0,091 est seulement la valeur approchée de A1A_1A1, à 10−310^{-3}10−3 près, par excès.De même,
A2=∫−1211−x2dx−∫−121(−33x+33)dx\displaystyle A_2=\int_{-\dfrac{1}{2}}^1 \sqrt{1-x^2}dx-\int_{-\dfrac{1}{2}}^1(-\dfrac{\sqrt 3}{3}x+\dfrac{\sqrt 3}{3})dx A2=∫−2111−x2dx−∫−211(−33x+33)dx
Avec les primitives usuelles, sauf erreur, après calculs, tu dois trouver
A2=π3−34\boxed{A_2=\dfrac{\pi}{3}-\dfrac{\sqrt 3}{4}}A2=3π−43
0,614 est seulement la valeur approchée de A2A_2A2 à 10−310^{-3}10−3 près, par défaut.Tu peux trouver des valeurs approchées des intégrales puis des deux aires A1A_1A1 et A2A_2A2 avec la méthode de Monté-Carlo , mais il faut faire un programme informatique pour que ça puisse donner des valeurs approchées convenables...
Je te mets un lien vers une explication très simple de la méthode avec un exemple de programme fait en Python.
Ce n'est peut-être pas le langage Python qui t'intéresse mais ça te permettra, j'espère, de comprendre la démarche.
https://www.youtube.com/watch?v=unkh3TZU3YM
Ensuite, il te faudra l'adapter au langage de programmation dont tu as l'habitude.
Bonjour @FANSI-Léo, une fois que tu as les valeurs exactes je pense qu'il te faut maintenant déterminer les conditions que tu devras utiliser dans ton algorithme, à savoir:
Quand est-ce qu'un point appartient à A1, et quand est-ce qu'un point appartient à A2. Une fois les intervalles bien définis, le reste c'est juste de la programmation de base à mon avis. Si tu n'es pas à l'aise avec Python tu peux toujours aller en C, C++, JAVA, etc. Le plus important c'est avoir ton algorithme bien définit.
-
mtschoon dernière édition par

De rien @FANSI-Léo , et bon courage pour ta programmation (dans le langage que tu connais)