Processus de Naissance et de mort (Processus de Markov)

Bonjour à tout le monde. J'espère que tous les membres de cette communauté se porte super bien.

Bon voilà, j'ai un exercice qui me turlupine depuis quelques jour.

Etude d’une population.
On souhaite observer l’évolution d’une espèce animale en voie de disparition. On possède les hypothèses suivantes :
• La population initiale est de 100 individus à parité sexuelle et d’âges uniformément répartis..
• Chaque couple donne par an en moyenne un enfant.
• La durée moyenne de vie d’un individu est de 3,5 ans.
On souhaite connaître ce que deviendra cette espèce dans 20 ans. Quelle est votre réponse ?

@LEFAJELE-LEFAJELE a dit dans Processus de Naissance et de mort (Processus de Markov) :

Bonjour à tout le monde. J'espère que tous les membres de cette communauté se porte super bien.

Bon voilà, j'ai un exercice qui me turlupine depuis quelques jour.

Etude d’une population.
On souhaite observer l’évolution d’une espèce animale en voie de disparition. On possède les hypothèses suivantes :
• La population initiale est de 100 individus à parité sexuelle et d’âges uniformément répartis..
• Chaque couple donne par an en moyenne un enfant.
• La durée moyenne de vie d’un individu est de 3,5 ans.
On souhaite connaître ce que deviendra cette espèce dans 20 ans. Quelle est votre réponse ?

Bonsoir tout le monde. J'espère que la communauté se porte super bien.
Bon voilà j'ai essayé de résoudre cet exercice en trouvant une suite ou une corrélation entre les évènements et voici ce que j'ai obtenu.

Posons U0 = 100 le nombre d'individus à l'année 0.
Après 1 an : U1 = U0 + 1/2U0 = 3/2U0 = 150.
(1/2U0 représentant le nombre de couple que l'on peut constituer à partir de U0)
Après 2 ans : U2 =U1 + 1/2U1 = 3/2U1 = (3/2)2U0 = 225.
Après 3 ans : U3 =U2 + 1/2U2 = 3/2U2 = (3/2)3U0 = 337.5.
Après 4 ans : 3.5 années se sont déjà écoulées et les individus nés au courant de l’année 0 meurent conforment à la moyenne de vie qui est 3.5 ans ainsi,
U4 = (U3 – U0) + 1/2 (U3–U0) = 3/2(U3 – U0) = 3/2(337.5 – 100)
U4 = 356.25
Après 5 ans : Les individus nés au courant de l’année 1 meurent et on a donc
U5 = (U4 – (U1 – U0)) + 1/2 (U4 – (U1–U0)) = 3/2(U4 – (U1 – U0))
U5 = 3/2(356.25 – (150 - 100)) = 459.375
Après 6 ans : Les individus nés au courant de l’année 2 meurent et on a donc
U6 = (U5 – (U2–U1)) + 1/2 (U5 – (U2–U1)) = 3/2(U5 – (U2 – U1))
U6 = 3/2(459.375 – (225 - 150)) = 576.5625
Après 7 ans : Les individus nés au courant de l’année 3 meurent et on a donc
U7 = (U6 – (U3–U2)) + 1/2 (U6 – (U3–U2)) = 3/2(U6 – (U3 – U2))
U7 = 3/2(576.5625 – (337.5 - 225)) = 696.09375
Après 8 ans : Les individus nés au courant de l’année 4 meurent et on a donc
U8 = (U7 – (U4–U3)) + 1/2(U7 – (U4–U3)) = 3/2(U7 – (U4 – U3))
U8 = 3/2(696.09375 – (356.25 – 337.5)) = 1016.015625
Ces résultats nous permettent donc de dire que
Pour n = 0, Un = 100 ;
Pour n dans l’intervalle ]0,3], Un = 3/2Un-1 ;
Pour n = 4, Un = 3/2U3 – U0 ;
Pour n ≥ 5, Un = 3/2[Un-1 – (Un-4 – Un-5)] ;
L’objectif de l’exercice étant de déterminer U20, il est nécessaire de mettre sur pied un programme de simulation basé sur les règles énumérées ci-haut pour déterminer Un, n étant égale 20 pour notre cas.

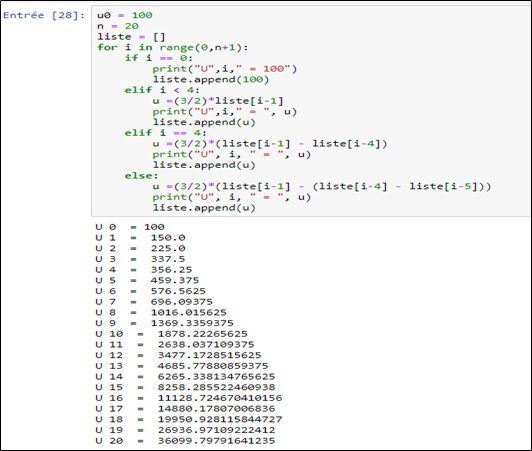
J'aimerai bien avoir vos avis et vos remarques

@LEFAJELE-LEFAJELE , bonjour,

Je regarde la suite que tu proposes.
Elle est tout à fait exacte mais elle ne semble pas tenir compte de toutes les indications données dans l'énoncé.

L'énoncé indique :
" La population initiale est de 100 individus à parité sexuelle et d’âges uniformément répartis"

La condition "d’âges uniformément répartis" ne semble pas intervenir dans tes calculs.
Vu que les âges de ces 100 individus doivent être uniformément répartis, il doit y en avoir :
25 nés au cours de l'année 0,
25 qui ont 1 an à l'année 0,
25 qui ont 2 ans à l'année 0,
25 qui ont 3 ans à l'année 0.

Tu as écrit " Posons U0 = 100 le nombre d'individus à l'année 0" ;
Dans les calculs qui suivent, tu sembles n'avoir tenu compte que des naissances durant les années 1,2,3. Il y a aussi des décès.
Par exemple, les 25 qui ont 3 ans à l'année 0, ne sont pas vivants à l'année 1.
Je me demande si tu n'as pas fait comme si les 100 individus de la population initiale, c'est à dire de l'année 0, étaient tous nés durant l'année 0.

Il me semble que tu devrais reprendre ta démarche pour pouvoir tenir compte de ces éléments.

Bon courage ... il en faut !

@LEFAJELE-LEFAJELE ,

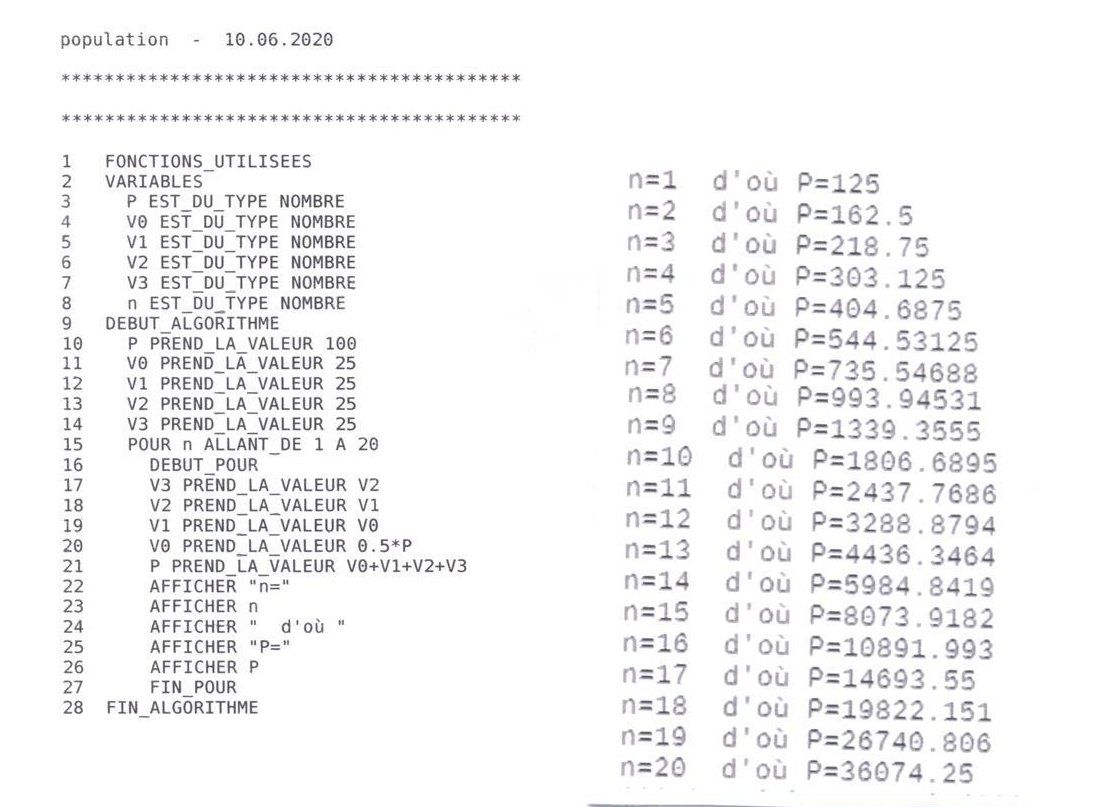
Je te suggère une démarche qui tient compte de toutes les hypothèses de l'énoncé.
P : effectif de la population une année n de N, décomposé en 4 parties :
V0 : effectif des individus naissant au cours de cette année n
V1 : effectif des individus ayant 1 an à cette année n
V2 : effectif des individus ayant 2 an à cette année n
V3 : effectif des individus ayant 3 an à cette année n
d'où P=V0+V1+V2+V3
Ainsi, on peut utiliser l'hypothèse relative à la répartition uniforme des âges de l'année 0
Je te joins un algorithme tapé avec Algobox (avec les résultats)
Pour les premières années, il y a une différence avec ta proposition (en fonction de l'hypothèse prise au départ), mais cette différence s'estompe au fil du temps, ce qui est logique.

Bonnes réflexions.