Calcul des coordonnées d'un sommet d'un triangle rectangle
-
Jerome Ksigzkiewiez dernière édition par Jerome Ksigzkiewiez
[0_1606406246525_exemple.png](Envoi en cours 100%)
Bonjour,
Suite a une réflexion avec des amis, nous nous somme retrouvé devant ce problème et nous n'avons pas trouver de solution.
Je me retourne donc vers vous pour que quelqu'un puisse me fournir une réponse.
Le problème est simple :
Imaginons 2 points sur un repère A et B, nous connaissons leurs coordonnées.
J'aimerais calculer les coordonnées d'un troisième point C, le triangle formé par ces 3 points (ABC) forme un triangle rectangle, rectangle en B.
La distance entre BC est de 1 (après c'est un détaille ça)Voila si quelqu'un a une idée pour résoudre ce problème, j'en serais très reconnaissant

(J'ai essayé d'ajouter une image, mais ça pas l'air de fonctionner.. )
-
mtschoon dernière édition par mtschoon

@Jerome-Ksigzkiewiez , bonsoir,
Effectivement, il y a un problème avec les images. Cela a été signalé.
Tu dois prendre le bouton "Image" et après avoir mis ton image chez un hébergeur d'images sur le web, ainsi avoir son URL, tu pourras l''utiliser.Si j'ai bien compris ta préoccupation, les points C cherchés seront situés sur la droite passant par B et perpendiculaire à (AB)
A condition que le repère soit orthonormé, je te conseille de passer par le produit scalaire : AB→.BC→=0\overrightarrow{AB}. \overrightarrow{BC}=0AB.BC=0
Tu auras l'équation de la droite (BC).
Ainsi tu pourras, par exemple, donner à l'abscisse de C une valeur de ton choix et l'équation de (BC) te permettra de trouver l'ordonnée de C correspondante.
AB→.BC→=0\overrightarrow{AB}. \overrightarrow{BC}=0AB.BC=0 équivaut à :
(xB−xA)(xC−xB)+(yB−yA)(yC−yB)=0\boxed{(x_B-x_A)(x_C-x_B)+(y_B-y_A)(y_C-y_B)=0}(xB−xA)(xC−xB)+(yB−yA)(yC−yB)=0 (Formule 1)Il te reste à remplacer xA,xB,yA,yBx_A,x_B,y_A,y_BxA,xB,yA,yB par leurs valeurs pour obtenir la relation entre xCx_CxC et yCy_CyC
Complément : si tu veux, en plus, que la distance BC soit de 1, il faut :
(xC−xB)2+(yC−yB)2=1\sqrt{(x_C-x_B)^2+(y_C-y_B)^2}=1(xC−xB)2+(yC−yB)2=1
C'est à dire, en élevant au carré :
(xC−xB)2+(yC−yB)2=1\boxed{(x_C-x_B)^2+(y_C-y_B)^2=1}(xC−xB)2+(yC−yB)2=1 (Formule 2)
(Ceci est l'équation du cercle de centre B et de rayon 1)Avec cette condition supplémentaire, tu obtiendras deux points solutions (C1C_1C1 et C2C_2C2) en résolvant le système composé des Formules 1 et 2.
-
mtschoon dernière édition par mtschoon

@Jerome-Ksigzkiewiez , je t'indique un exemple, si besoin
xA=0.5x_A=0.5xA=0.5 et yA=1y_A=1yA=1
xB=1.5x_B=1.5xB=1.5 et yB=2y_B=2yB=2Avec la Formule 1, après calcul, tu dois trouver :
xC+yC−3.5=0x_C+y_C-3.5=0xC+yC−3.5=0
(C'est l'équation de la droite (Δ))(\Delta))(Δ))Avec la Formule 2, après calcul, tu dois trouver
(xC−1.5)2+(yC−2)2=1(x_C-1.5)^2+(y_C-2)^2=1(xC−1.5)2+(yC−2)2=1
(C'est l'équation du cercle de centre B et de rayon 1)Tu dois résoudre le système
{xC+yC−3.5=0(xC−1.5)2+(yC−2)2=1\begin{cases}x_C+y_C-3.5=0 \cr (x_C-1.5)^2+(y_C-2)^2=1 \end{cases}{xC+yC−3.5=0(xC−1.5)2+(yC−2)2=1yC=−xC+3.5y_C=-x_C+3.5yC=−xC+3.5
Tu substitues dans la seconde équation, qui devient :
(xC−1.5)2+(−xC+3.5−2)2=1(x_C-1.5)^2+(-x_C+3.5-2)^2=1(xC−1.5)2+(−xC+3.5−2)2=1
c'est à dire :
(xC−1.5)2+(−xC+1.5)2=1(x_C-1.5)^2+(-x_C+1.5)^2=1(xC−1.5)2+(−xC+1.5)2=1Après calcul, cette équation s'écrit :
2(xC)2−6xC+3.5=02(x_C)^2-6x_C+3.5=02(xC)2−6xC+3.5=0
C'est une équation du second degré que tu résous avec les formules usuelles.
Tu dois trouver deux solutions
xC1=3+22x_{C_1}=\dfrac{3+\sqrt 2}{2}xC1=23+2 et xC2=3−22x_{C_2}=\dfrac{3-\sqrt 2}{2}xC2=23−2En remplaçant dans yC=−xC+3.5y_C=-x_C+3.5yC=−xC+3.5 , tu obtiens
yC1=4−22y_{C_1}=\dfrac{4-\sqrt 2}{2}yC1=24−2 et yC2=4+22y_{C_2}=\dfrac{4+\sqrt 2}{2}yC2=24+2Tu as ainsi les coordonnées exactes des deux points C solutions.
Je t'indique des valeurs approchées, si tu veux vérifier sur le graphique :
xC1≈2.207x_{C_1} \approx 2.207xC1≈2.207
yC1≈1.292y_{C_1} \approx 1.292yC1≈1.292
xC2≈0.792x_{C_2} \approx 0.792xC2≈0.792
yC2≈2.707y_{C_2} \approx 2.707yC2≈2.707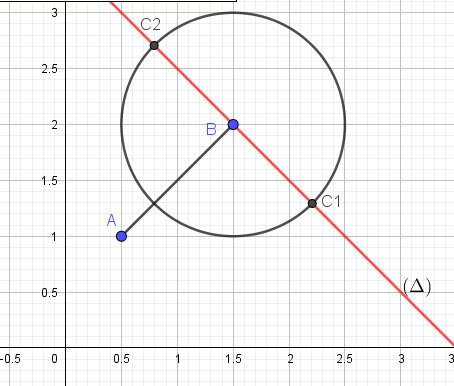
Bonne lecture !
-
Jerome Ksigzkiewiez dernière édition par
Bonjour !
Wow, je te remercie pour le temps que tu as pris pour moi, surtout merci pour tes réponses plus que détaillées.
Il va falloir que je prennent du temps pour assimilé tout cela, mais c'est très clair, et on était très loin de trouver la réponse avec mes amis x)
-
mtschoon dernière édition par

@Jerome-Ksigzkiewiez , de rien , c'est avec plaisir !
Reposte si quelques détails t'échappent.