Les assertions, vraies ou fausses

[Wil Fried]

Bonsoir, veuillez m'éclairer svp!
Pour chacune des questions suivantes indiquées si l’assertion est vraie ou fausse.

1. Il existe des fonctions numériques d’une variable réelle définies en tout point et
   continues en aucun. Si l’assertion est vraie, donner un exemple.
2. Toute fonction numérique d’une variable réelle qui admet une dérivée première
   continue est deux fois dérivable.

A la première j'ai répondu FAUX!
A la deuxième j'ai répondu également FAUX!
Êtes vous d'accord avec moi ?
Je veux avoir des explications sur ce genre d'exercice et leurs résolutions. Car moi j'ai simplement répondu soit par V ou par F.

[mtschoon]

@Wil-Fried , bonjour,

Bien sûr, pour donner un réponse VRAI ou FAUX, il faut savoir pourquoi...

Pour la première assertion, tu peux donner l'exemple (historique) de fonction de Dirichlet
Tu peux trouver des documentations sur le web

Soit $Q$ l'ensemble des rationnels et $R/Q$ l'ensemble des irrationnels.
Il y a un rationnel entre deux irrationnels.

Soit f la fonction définie par :
Pour x rationnel, $x\in Q$ , $f(x)=1$
Pour x irrationnel, $x\in R/Q$, $f(x)=0$

Cette fonction numérique d’une variable réelle est définie en tout point et continue en aucun.

Pour justifier qu'il y a un rationnel entre deux irrationnels, regarde le lien ici :
https://www.youtube.com/watch?v=uXUhws-OaM4

Tu tires la conclusion.

[mtschoon]

@Wil-Fried , je regarde la seconde assertion proposée.

Je ne trouve pas la question précise car on ne sait pas trop sur quel ensemble on travaille.

Je t'indique un exemple possible de fonction $f$ définie sur $R$, dérivable sur $R$, dont la dérivée $f^{\prime }$ est continue sur $R$ mais telle que $f^{\prime }$ n'est pas dérivable sur tout $R$ (donc $f$ n'est pas deux fois dérivable sur tout $R$)

Soit f définie par :
$f(0)=0$
Pour $x>0$, $f(x)=x^2$
Pour $x<0$ ,$f(x)=-x^2$

Tu peux prouver que f est dérivable sur R et que
$f^{\prime }(0)=0$
Pour $x>0$, $f^{\prime }(x)=2x$
Pour $x<0$ ,$f(x)=-2x$

Cette fonction $f^{\prime }$ peut s'écrire, pour tout $x$ de $R$ : $f^{\prime }(x)=2|x|=|2x|$

Cette fonction $f^{\prime }$ est bien continue sur $R$ mais elle n'est pas dérivable sur tout $R$ car elle n'est pas dérivable en $0$

Tu tires la conclusion.

Tu peux bien sûr, trouver des exemples personnels.

[mtschoon]

@Wil-Fried ,

Pour illustrer l'exemple que je viens de t'indiquer ( pour ta seconde assertion) , je te mets la représentation graphique de $f$ (en rouge) et de $f$'(en bleu)

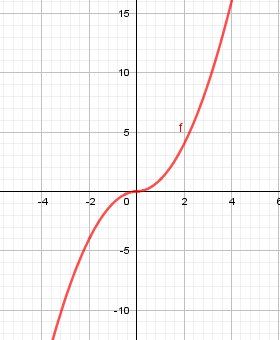
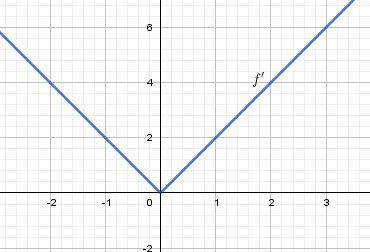
($f^{\prime }$ n'est pas dérivable en 0, car en $0$ le nombre dérivé à gauche vaut $-1$ et le nombre dérivé à droite vaut $+1$ et $-1\ne +1$

[Wil Fried]

@mtschoon Merci pour l'exemple!
Moi j'avais répondu comme suit ( à la deuxième assertion bien sûr) : Faux car la continuité n'entraîne pas la dérivabilité.

[mtschoon]

De rien @Wil-Fried ,
A l'assertion 1, il fallait répondre Oui (cas de la fonction de Dirichlet, par exemple).

A l'assertion 2, il fallait répondre Non et ton idée est bonne. C'est suffisant si un exemple n'est pas exigé.